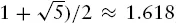Mathematics in Nature

Modeling Patterns in the Natural World

John Adam

• Publisher: Princeton University Press
• Year: 2011
• ISBN:
  9781400841011
• Topic: Mathematics
• Subtopic: Games in Mathematics
• Index: Mathematics

From rainbows, river meanders, and shadows to spider webs, honeycombs, and the markings on animal coats, the visible world is full of patterns that can be described mathematically. Examining such readily observable phenomena, this book introduces readers to the beauty of nature as revealed by mathematics and the beauty of mathematics as revealed in nature.
Generously illustrated, written in an informal style, and replete with examples from everyday life, Mathematics in Nature is an excellent and undaunting introduction to the ideas and methods of mathematical modeling. It illustrates how mathematics can be used to formulate and solve puzzles observed in nature and to interpret the solutions. In the process, it teaches such topics as the art of estimation and the effects of scale, particularly what happens as things get bigger. Readers will develop an understanding of the symbiosis that exists between basic scientific principles and their mathematical expressions as well as a deeper appreciation for such natural phenomena as cloud formations, halos and glories, tree heights and leaf patterns, butterfly and moth wings, and even puddles and mud cracks.
Developed out of a university course, this book makes an ideal supplemental text for courses in applied mathematics and mathematical modeling. It will also appeal to mathematics educators and enthusiasts at all levels, and is designed so that it can be dipped into at leisure.

CHAPTER ONE

The Confluence of Nature
and Mathematical Modeling

Great are the works of the Lord; they are pondered by all who delight in them.

—Psalm 111:2

CONFLUENCE . . .

In recent years, as I have walked daily to and from work, I have started to train myself to observe the sky, the birds, butterflies, trees, and flowers, something I had not done previously in a conscious way (although I did watch out for fast-moving cars and unfriendly dogs). Despite living in suburbia, I find that there are many wonderful things to see: clouds exhibiting wave-like patterns, splotches of colored light some 22 degrees away from the sun (sundogs, or parhelia), wave after wave of Canada geese in “vee” formation, the way waves (and a following region of calm water) spread out on the surface of a puddle as a raindrop spoils its smooth surface, the occasional rainbow arc, even the iridescence on the neck of those rather annoying birds, pigeons, and many, many more nature-given delights. And so far I have not been late for my first class of the morning!

The idea for this book was driven by a fascination on my part for the way in which so many of the beautiful phenomena observable in the natural realm around us can be described in mathematical terms (at least in principle). What are some of these phenomena? Some have been already mentioned in the preface, but for a more complete list we might consider rainbows, “glories,” halos (all atmospheric occurrences), waves in air, earth, oceans, rivers, lakes, and puddles (made by wind, ship, or duck), cloud formations (billows, lee waves), tree and leaf branching patterns (including phyllotaxis), the proportions of trees, the wind in the trees, mud-crack patterns, butterfly markings, leopard spots, and tiger stripes. In short, if you can see it outside, and a human didn’t make it, it’s probably described here! That, of course, is an exaggeration, but this book does attempt to answer on varied levels the fundamental question: what kind of scientific and mathematical principles undergird these patterns or regularities that I claim are so ubiquitous in nature?

Two of the most fundamental and widespread phenomena that occur in the realm of nature are the scattering of light and wave motion. Both may occur almost anywhere given the right circumstances, and both may be described in mathematical terms at varying levels of complexity. It is, for example, the scattering of light both by air molecules and by the much larger dust particles (or more generally, aerosols) that gives the amazing range of color, hues, and tints at sunrise or sunset that give us so much pleasure. The deep blue sky above and the red glow near the sun at the end of the day are due to molecular scattering of light, though dust or volcanic ash can render the latter quite spectacular at times.

The rainbow is formed by sunlight scattered in preferential directions by near-spherical raindrops: scattering in this context means refraction and reflection (although there many other fascinating features of light scattering that will not be discussed in great detail here). Using a simple mathematical description of this phenomenon, René Descartes in 1637 was able to “hang the rainbow in the sky” (i.e., deduce its location relative to the sun and observer), but to “paint” the rainbow required the genius of Isaac Newton some thirty years later. The bright primary and fainter secondary bows are well described by elementary mathematics, but the more subtle observable features require some of the most sophisticated techniques of mathematical physics to explain them. A related phenomenon is that of the “glory,” the set of colored, concentric rainbow-like rings surrounding, for example, the shadow of an airplane on a cloud below. This, like the rainbow, is also a “backscatter” effect, and, intriguingly, both the rainbow and the glory have their counterparts in atomic and nuclear physics; mathematics is a unifying feature between these two widely differing contexts. The beautiful (and commonly circular) arcs known as halos, no doubt seen best in arctic climes, are formed by the refraction of sunlight through ice crystals of various shapes in the upper atmosphere. Sundogs, those colored splashes of light often seen on both sides of the sun when high cirrus clouds are present, are similarly formed.

Like the scattering of light, wave motion is ubiquitous, though we cannot always see it directly. It is manifested in the atmosphere, for example, by billow clouds and lee-wave clouds downwind from a hill or mountain. Waves on the surface of puddles, ponds, lakes, or oceans are governed by mathematical relationships between their speed, their wavelength, and the depth of the water. The wakes produced by ships or ducks generate strikingly similar patterns relative to their size; again, this correspondence is described by mathematical expressions of the physical laws that govern the motion. The situation is even more complex in the atmosphere: the “compressible” nature of a gas renders other types of wave motion possible. Sand dunes are another complex and beautiful example of waves. They can occur on a scale of centimeters to kilometers, and, like surface waves on bodies of water, it is only the waveform that actually moves; the body of sand is stationary (except at the surface).

In the plant world, the arrangement of leaves around a stem or seeds in a sunflower or daisy face shows, in the words of one mathematician (H.S.M. Coxeter), “a fascinatingly prevalent tendency” to form recurring numerical patterns, studied since medieval times. Indeed, these patterns are intimately linked with the “golden number” ((

) so beloved of Greek mathematicians long ago. The spiral arrangement of seeds in the daisy head is found to be present in the sweeping curve of the chambered nautilus shell and on its helical counterpart, the Cerithium fasciatum (a thin, pointy shell). The curl of a drying fern and the rolled-up tail of a chameleon all exhibit types of spiral arc.

In the animal and insect kingdoms, coat patterns (e.g., on leopards, cheetahs, tigers, and giraffes) and wing markings (e.g., on butterflies and moths) can be studied using mathematics, specifically by means of the properties and solutions of so-called reaction-diffusion equations (and other types of mathematical models). Reaction-diffusion equations describe the interactions between chemicals (“activators” and “inhibitors”) that, depending on conditions, may produce spots, stripes, or more “splodgy” patterns. There are fascinating mathematical problems involved in this subject area, and also links with topics such as patterns on fish (e.g., angel fish) and seashells. In view of earlier comments, seashells combine both the effects of geometry and pattern formation mechanisms, and mathematical models can reproduce the essential features observed in many seashells.

Cracks also, whether formed in drying mud, tree bark, or rapidly cooling rock, have their own distinctive mathematical patterns; frequently they are hexagonal in nature. River meanders, far from being “accidents” of nature, define a form in which the river does the least work in turning (according to one class of models), which then defines the most probable form a river can take—no river, regardless of size, runs straight for more than ten times its average width.

Many other authors have written about these patterns in nature. Ian Stewart has noted in his popular book Nature’s Numbers that “We live in a universe of patterns. . . . No two snowflakes appear to be the same, but all possess six-fold symmetry.” Furthermore, he states that

there is a formal system of thought for recognizing, classifying and exploiting patterns. . . . It is called mathematics. Mathematics helps us to organize and systemize our ideas about patterns; in so doing, not only can we admire and enjoy these patterns, but also we can use them to infer some of the underlying principles that govern the world of nature. . . . There is much beauty in nature’s clues, and we can all recognize it without any mathematical training. There is beauty too in the mathematical stories that . . . deduce the underlying rules and regularities, but it is a different kind of beauty, applying to ideas rather than things. Mathematics is to nature as Sherlock Holmes is to evidence.

We may go further by asking questions like those posed by Peter S. Stevens in his lovely book Patterns in Nature. He asks,

Why does nature appear to use only a few fundamental forms in so many different contexts? Why does the branching of trees resemble that of arteries and rivers? Why do crystal grains look like soap bubbles and the plates of a tortoise shell? Why do some fronds and fern tips look like spiral galaxies and hurricanes? Why do meandering rivers and meandering snakes look like the loop patterns in cables? Why do cracks in mud and markings on a giraffe arrange themselves like films in a froth of bubbles?

He concludes in part that “among nature’s darlings are spirals, meanders, branchings, hexagons, and 137.5 degree angles. . . . Nature’s productions are shoestring operations, encumbered by the constraints of three-dimensional space, the necessary relations among the size of things, and an eccentric sense of frugality.

In the book By Nature’s Design, Pat Murphy expresses similar sentiments, writing,

Nature, in its elegance and economy, often repeats certain forms and patterns . . . like the similarity between the spiral pattern in the heart of a daisy and the spiral of a seashell, or the resemblance between the branching pattern of a river and the branching pattern of a tree . . . ripples that flowing water leaves in the mud . . . the tracings of veins in an autumn leaf . . . the intricate cracking of tree bark . . . the colorful splashings of lichen on a boulder. . . . The first step to understanding—and one of the most difficult—is to see clearly. Nature modifies and adapts these basic patterns as needed, shaping them to the demands of a dynamic environment. But underlying all the modifications and adaptations is a hidden unity. Nature invariably seeks to accomplish the most with the least—the tightest fit, the shortest path, the least energy expended. Once you begin to see these basic patterns, don’t be surprised if your view of the natural world undergoes a subtle shift.

Another fundamental (and philosophical) question has been asked by many—How can it be that mathematics, a product of human thought independent of experience, is so admirably adapted to the objects of reality? This fascinating question I do not address here; let it suffice to note that, hundreds of years ago, Galileo Galilei stated that the Universe “cannot be read until we have learnt the language and become familiar with the characters in which it is written. It is written in mathematical language.” Mathematics is certainly the language of science, but it is far, far more than a mere tool, however valuable, for it is of course both a subject and a language in its own right. But lest any of us should balk at the apparent need for speaking a modicum of that language in order more fully to appreciate this book, the following reassuring statement from Albert Einstein, when writing to a young admirer at junior high school, should be an encouragement. He wrote “Do not worry about your difficulties in mathematics. I can assure you that mine are still greater.” Obviously anyone, even scientists of great genius, can have difficulties in mathematics (one might add that it’s all a matter of relativity in this regard).

Obviously a significant component of this book is the application of elementary mathematics to the natural world around us. As I have tried to show already, there are many mathematical patterns in the natural world that are accessible to us if we keep our eyes and ears open; indeed, the act of “asking questions of nature” can lead to many fascinating “thought trails,” even if we do not always come up with the correct answers. First, though, let me remind you (unnecessarily, I am sure) that no one has all the answers to such questions. This is true for me at all times, of course (not just as a parent and a professor), but especially so in a subject as all-encompassing as “mathematics in nature.” There will always be “displays” or phenomena in nature that any given individual will be unable to explain to the satisfaction of everyone, for the simple reason that none of us is ever in possession of all the relevant facts, physical intuition, mathematical techniques, or other re...