Modeling Infectious Diseases in Humans and Animals

Matt J. Keeling, Pejman Rohani

• Publisher: Princeton University Press
• Year: 2011
• ISBN:
  9781400841035
• Topic: Ciencias biológicas
• Subtopic: Biología

For epidemiologists, evolutionary biologists, and health-care professionals, real-time and predictive modeling of infectious disease is of growing importance. This book provides a timely and comprehensive introduction to the modeling of infectious diseases in humans and animals, focusing on recent developments as well as more traditional approaches.Matt Keeling and Pejman Rohani move from modeling with simple differential equations to more recent, complex models, where spatial structure, seasonal "forcing, " or stochasticity influence the dynamics, and where computer simulation needs to be used to generate theory. In each of the eight chapters, they deal with a specific modeling approach or set of techniques designed to capture a particular biological factor. They illustrate the methodology used with examples from recent research literature on human and infectious disease modeling, showing how such techniques can be used in practice. Diseases considered include BSE, foot-and-mouth, HIV, measles, rubella, smallpox, and West Nile virus, among others. Particular attention is given throughout the book to the development of practical models, useful both as predictive tools and as a means to understand fundamental epidemiological processes. To emphasize this approach, the last chapter is dedicated to modeling and understanding the control of diseases through vaccination, quarantine, or culling.

• Comprehensive, practical introduction to infectious disease modeling
• Builds from simple to complex predictive models
• Models and methodology fully supported by examples drawn from research literature
• Practical models aid students' understanding of fundamental epidemiological processes
• For many of the models presented, the authors provide accompanying programs written in Java, C, Fortran, and MATLAB
• In-depth treatment of role of modeling in understanding disease control

Chapter One

Introduction

This book is designed as an introduction to the modeling of infectious diseases. We start with the simplest of mathematical models and show how the inclusion of appropriate elements of biological complexity leads to improved understanding of disease dynamics and control. Throughout, our emphasis is on the development of models, and their use either as predictive tools or as a means of understanding fundamental epidemiological processes. Although many theoretical results can be proved analytically for very simple models, we have generally focused on results obtained by computer simulation, providing analytical results only where they lead to a more generic interpretation of model behavior. Where practical, we have illustrated the general modeling principles with applied examples from the recent literature. We hope this book motivates readers to develop their own models for diseases of interest, expanding on the model frameworks given here.

1.1. TYPES OF DISEASE

The Oxford English Dictionary defines a disease as “a condition of the body, or of some part or organ of the body, in which its functions are disturbed or deranged; a morbid physical condition; a departure from the state of health, especially when caused by structural change.” This definition encompasses a wide range of ailments from AIDS to arthritis, from the common cold to cancer. The fine-scale classification of diseases varies drastically between different scientific disciplines. Medical doctors and veterinary clinicians, for example, are primarily interested in treating human patients or animals and, as such, are most concerned about the infection’s pathophysiology (affecting, for example, the central nervous system) or clinical symptoms (for example, secretory diarrhea). Microbiologists, on the other hand, focus on the natural history of the causative organism: What is the etiological agent (a virus, bacterium, protozoan, fungus, or prion)? and what are the ideal conditions for its growth? Finally, epidemiologists are most interested in features that determine patterns of disease and its transmission.

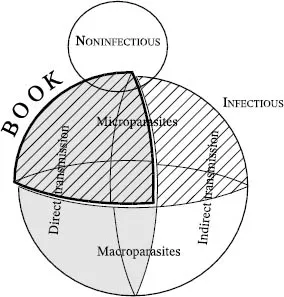
In general terms, we may organize diseases according to several overlapping classifications (Figure 1.1). Diseases can be either infectious or noninfectious. Infectious diseases (such as influenza) can be passed between individuals, whereas noninfectious diseases (such as arthritis) develop over an individual’s lifespan. The epidemiology of noninfectious diseases is primarily a study of risk factors associated with the chance of developing the disease (for example, the increased risk of lung cancer attributable to smoking). In contrast, the primary risk factor for catching an infectious disease is the presence of infectious cases in the local population—this tenet is reflected in all the mathematical models presented in this book. These two categories, infectious and noninfectious, are not necessarily mutually exclusive. Infection with the human papillomavirus (HPV), for example, is firmly associated with (although not necessary for developing) cervical cancer, thus bridging the two fields. This book focuses on infectious diseases, where models have great predictive power at the population scale and over relatively short time scales.

Figure 1.1. A representation of the various types of diseases. The two main groups of infectious and noninfectious diseases are represented by the two circles. The infectious group can be further subdivided into directly transmitted (gray) and indirectly transmitted infections as well as into diseases due to microparasites (hatched) and macroparasites. The focus of this book are the diseases subsumed within the intersection of the hatched and gray areas, which is offset and bounded by a thick black line.

Infectious diseases can be further subdivided (Figure 1.1). The infecting pathogen can be either a microparasite (hatched in diagram) or a macroparasite. Microparasites, as the same suggests, are small (usually single-cell organisms) and are either viruses, bacteria, protoza, or prions; macroparasites are any larger form of pathogen and include helminths and flukes. Although the biological distinction between these two groups of organisms is clear, from a modeling perspective the boundaries are less well defined. In general, microparasitic infections develop rapidly from a small number of infecting particles so the internal dynamics of the pathogen within the host can often be safely ignored. As a result, we are not interested in the precise abundance of pathogens within the host; instead we focus on the host’s infection status. In contrast, macroparasites such as helminths have a complex life cycle within the host which often needs to be modeled explicitly. In addition, the worm burden, or the number of parasites within the host, represents an important contributing factor to pathogenicity and disease transmission. We focus in this book on microparasites, where extensive long-term data and a good mechanistic understanding of the transmission dynamics have led to a wealth of well-parameterized models.

Infectious diseases (both macro-and microparasitic) can also be subdivided into two further categories (Figure 1.1), depending on whether transmission of infection is direct (shaded gray) or indirect. Direct transmission is when infection is caught by close contact with an infectious individual. The great majority of microparasitic diseases, such as influenza, measles, and HIV, are directly transmitted, although there are exceptions such as cholera, which is waterborne. Generally, directly transmitted pathogens do not survive for long outside the host organism. In contrast, indirectly transmitted parasites are passed between hosts via the environment; most macroparasitic diseases, such as those caused by helminths and schistosomes, are indirectly transmitted, spending part of their life cycle outside of their hosts. In addition, there is a class of diseases where transmission is via a secondary host or vector, usually insects such as mosquitoes, tsetse flies, or ticks. However, this transmission route can be considered as two sequential direct transmission events, from the primary host to the insect and then from the insect to another primary host.

The models and diseases of this book are focused toward the study of directly transmitted, microparasitic infectious diseases. As such, this subset represents only a fraction of the whole field of epidemiological modeling and analysis, but one in which major advances have occurred over recent decades.

Worldwide there are about 1,415 known human pathogens of which 217 (15%) are viruses or prions and 518 (38%) are bacteria or rickettsia; hence around 53% are micro-parasites (Cleaveland et al. 2001). Of these pathogens, 868 (61%) are zoonotic and can therefore be transmitted from animals to humans. Around 616 pathogens of domestic livestock are known, of which around 18% are viral and 25% bacterial. However, if we restrict our attention to the 70 pathogens listed by the Office International des Epizooties (which contain the most prominent and infectious livestock diseases), we find that 77% are microparasites (Cleaveland et al. 2001). The lower number of known livestock pathogens compared to human pathogens probably reflects to some degree our natural anthropocentric bias. Similarly, very few infectious diseases of wildlife are known or studied in any detail, and yet wildlife reservoirs may be important sources of novel emerging human infections. It is therefore clear that the study of microparasitic infectious diseases encompasses a huge variety of hosts and diseases.

1.2. CHARACTERIZATION OF DISEASES

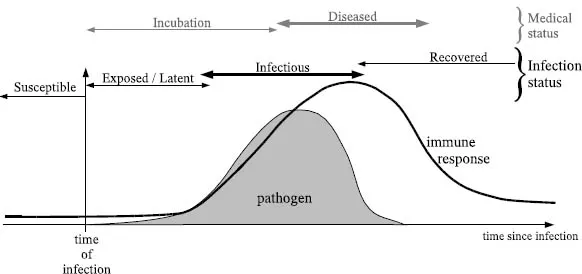
The progress of an infectious microparasitic disease is defined qualitatively in terms of the level of pathogen within the host, which in turn is determined by the growth rate of the pathogen and the interaction between the pathogen and the host’s immune response. Figure 1.2 shows a much simplified infection profile. Initially, the host is susceptible to infection: No pathogen is present; just a low-level nonspecific immunity within the host. At time 0, the host encounters an infectious individual and becomes infected with a microparasite; the abundance of the parasite grows over time. During this early phase the individual may exhibit no obvious signs of infection and the abundance of pathogen may be too low to allow further transmission—individuals in this phase are said to be in the exposed class. Once the level of parasite is sufficiently large within the host, the potential exists to transmit the infection to other susceptible individuals; the host is infectious. Finally, once the individual’s immune system has cleared the parasite and the host is therefore no longer infectious, they are referred to as recovered.

This fundamental classification (as susceptible, exposed, infectious, or recovered) solely depends on the host’s ability to transmit the pathogen. This has two implications. First, the disease status of the host is irrelevant—it is not important whether the individual is showing symptoms; an individual who feels perfectly healthy can be excreting large amounts of pathogen (Figure 1.2). Second, the boundaries between exposed and infectious (and infectious and recovered) are somewhat fuzzy because the ability to transmit does not simply switch on and off. This uncertainty is further complicated by the variability in responses between different individuals and the variability in pathogen levels over the infectious period; it is only with the recent advances in molecular techniques that these within-host individual-level details are beginning to emerge. Our classification of hosts as susceptible, exposed, infectious, or recovered can therefore be compared to the ecological concept of a metapopulation (Levins 1969; Hanski and Gilpin 1991), in which the within-host density of the pathogen is ignored and each host is simply classified as being in one of a limited number of categories.

Figure 1.2. A caracature of the time-line of infection, showing the dynamics of the pathogen (gray area) and the host immune response (black line) as well as labeling the various infection classes: susceptible, exposed, infectious, and recovered. Note that the diseased period, when symptoms are experienced, is not necessarily correlated with any particular infection class.

Although Figure 1.2 shows an example of a disease profile that might be modeled as SEIR (susceptible-exposed-infectious-recovered), other within-host profiles are also common. Often, it is mathematically simpler and justifiable at the population scale to ignore the exposed class, reducing the number of equations by one and leading to SIR dynamics. Some infections, especially of plants, are more appropriately described by the SI (susceptible-infectious) paradigm; for such diseases, the host is infectious soon after it is infected, such that the exposed period can be safely ignored, and remains infectious until its death. Other infectious diseases, in particular sexually transmitted infections (such as gonorrhoea), are better described by an SIS (susceptible-infectious-susceptible) framework, because once recovered (or following treatment) the host is once again susceptible to infection. In the majority of cases this renewed susceptibility is due to the vast antigenic variation associated with sexually transmitted diseases. Finally, many diseases have profiles that are individualistic and require specific model formulation. Smallpox has a definite short prodromal period before the symptoms emerge when the infected individual is mobile and can widely disseminate the virus but infectiousness has not reached its peak. Hepatitis B has a carrier state such that some infected individuals do not fully recover but transmit at a low level for the rest of their lives. Chlamydia (and many other sexually transmitted diseases) may be asymptomatic, such that some infected individuals do not suffer from the disease even though they are able to transmit infection. Similarly, infections such as meningitis or MRSA (methicillin resistant streptococus aurius) are widespread in the general population and usually benign, with only occasional symptomatic outbreaks. All of these more complex epidemiological behaviors require greater subdivision of the population and therefore models that deal explicitly with these extra classes.

Although such qualitative descriptions of disease dynamics allow us to understand the behavior of infection within an individual and may even shed some light on potential transmission, if we are to extrapolate from the individual-level dynamics to the population-scale epidemic, numerical values are required for many of the key parameters. Two fundamental quantities govern the population-level epidemic dynamics: the basic reproductive ratio, R₀, and the timescale of infection, which is measured by the infectious period for SIS and SIR infections or by a mixture of exposed and infectious periods in diseases with SEIR dynamics (for details, see Chapter 2). The basic reproductive ratio is one of the most critical epidemiological parameters because it defines the average number of secondary cases an average primary case produces in a totally susceptible population. Among other things, this single parameter allows us to determine whether a disease can successfully invade or not, the threshold level of vaccination required for eradication, and the long-term proportion of susceptible individuals when the infection is endemic.

One of the key features of epidemiological modeling is the huge variability in infection profiles, parameter values, and timescales. Many childhood infectious diseases (such as measles, rubella, or chickenpox) follow the classic SEIR profile, have high basic reproductive ratios (R₀ ≈ 17 for both measles and whooping cough in England and Wales from 1945 to 1965), and short infected periods (of less than one month). In contrast, diseases such as HIV have a much more complex infection profile with transmission rates varying as a function of time since infection, R0 is crucially dependent on sexual behavior (R₀ ≈ 4 for the homosexual population in the United Kingdom, whereas R₀ ≈ 11 for female prostitutes in Kenya), and infection is lifelong. Between these two extremes lies a vast array of other infectious diseases, with their own particular characteristics and parameters.

1.3. CONTROL OF INFECTIOUS DISEASES

One of the primary reasons for studying infectious diseases is to improve control and ultimately to eradicate the infection from the population. Models can be a powerful tool in this approach, allowing us to optimize the use of limited resources or simply to target control measures more efficiently. Several forms of control measure exist; all operate by reducing the average amount of transmission between infectious and susceptible individuals. Which control strategy (or mixture of strategies) is used will depend on the disease, the hosts, and the scale of the epidemic.

The practice of vaccination began with Edward Jenner in 1796 who developed a vaccine against smallpox—which remains the only disease to date that has been eradicated world-wide. Vaccination acts by stimulating a host immune response, such that immunized individuals are protected against infection. Vaccination is generally applied prophylactically to a large proportion of the population, so as to greatly reduce the number of susceptible individuals. Such prophylactic vaccination campaigns have successfully reduced the incidence of many childhood infections in the developed world by vaccinating the vast majority of young children and infants. In 1988, the World Heath Organization (WHO) resolved to use similar campaigns to eradicate polio worldwide by 2005—this is still ongoing work although muc...