When Least Is Best

How Mathematicians Discovered Many Clever Ways to Make Things as Small (or as Large) as Possible

Paul Nahin

• Publisher: Princeton University Press
• Year: 2011
• Print ISBN: 9780691130521, 9780691070780
• eBook ISBN: 9781400841363
• Topic: Mathematics
• Subtopic: History & Philosophy of Mathematics
• Index: Mathematics

What is the best way to photograph a speeding bullet? Why does light move through glass in the least amount of time possible? How can lost hikers find their way out of a forest? What will rainbows look like in the future? Why do soap bubbles have a shape that gives them the least area?

By combining the mathematical history of extrema with contemporary examples, Paul J. Nahin answers these intriguing questions and more in this engaging and witty volume. He shows how life often works at the extremes--with values becoming as small (or as large) as possible--and how mathematicians over the centuries have struggled to calculate these problems of minima and maxima. From medieval writings to the development of modern calculus to the current field of optimization, Nahin tells the story of Dido's problem, Fermat and Descartes, Torricelli, Bishop Berkeley, Goldschmidt, and more. Along the way, he explores how to build the shortest bridge possible between two towns, how to shop for garbage bags, how to vary speed during a race, and how to make the perfect basketball shot.

Written in a conversational tone and requiring only an early undergraduate level of mathematical knowledge, When Least Is Best is full of fascinating examples and ready-to-try-at-home experiments. This is the first book on optimization written for a wide audience, and math enthusiasts of all backgrounds will delight in its lively topics.

1.

Minimums, Maximums,
Derivatives, and
Computers

1.1 Introduction

This book has been written from the practical point of view of the engineer, and so you’ll see few rigorous proofs on any of the pages that follow. As important as such proofs are in modern mathematics, I make no claims for rigor in this book (plausibility and/or direct computation are the themes here), and if absolute rigor is what you are after, well, you have the wrong book. Sorry!

Why, you may ask, are engineers interested in minimums? That question could be given a very long answer, but instead I’ll limit myself to just two illustrations (one serious and one not, perhaps, quite as serious). Consider first the problem of how to construct a gadget that has a fairly short operational lifetime and which, during that lifetime, must perform flawlessly. Short lifetime and low failure probability are, as is often the case in engineering problems, potentially conflicting specifications: the first suggests using low-cost material(s) since the gadget doesn’t last very long, but using cheap construction may result in an unacceptable failure rate. (An example from everyday life is the ordinary plastic trash bag—how thick should it be? The bag is soon thrown away, but we definitely will be unhappy if it fails too soon!) The trash bag engineer needs to calculate the minimum thickness that still gives acceptable performance.

For my second example, let me take you back to May 1961, to the morning the astronaut Alan Shepard lay on his back atop the rocket that would make him America’s first man in space. He was very brave to be there, as previous unmanned launches of the same type of rocket had shown a disturbing tendency to explode into stupendous fireballs. When asked what he had been thinking just before blastoff, he replied “I was thinking that the whole damn thing had been built by the lowest bidder.”

This book is a math history book, and the history of minimums starts centuries before the time of Christ. So, soon, I will be starting at the beginning of our story, thousands of years in the past. But before we climb into our time machine and travel back to those ancient days, there are a few modern technical issues I want to address first.

First, to write a book on minimums might seem to be a bit narrow; why not include maximums, too? Why not write a history of extremas, instead? Well, of course minimums and maximums are indeed certainly intimately connected, since a maximum of y(x) is a minimum of -y(x). To be honest, the reason for the book’s title is simply that I couldn’t think of one I could use with extrema as catchy as is “When Least Is Best.” I did briefly toy with “When Extrema Are xxx” with the xxx replaced with exotic, exciting, and even (for a while, in a temporary fit of marketing madness that I hoped would attract Oprah’s attention), erotic. Or even “Minimums Are from Venus, Maximums Are from Mars.” But all of those (certainly the last one) are dumb, and so it stayed “When Least Is Best.” There will be times, however, when I will discuss maximums, too. And now and then we’ll use a computer as well.

For example, consider the problem of finding the maximum value of the rather benign-looking function

.

Some students answer too quickly and declare the maximum value is 8, believing that for some value of x the individual maximums of the two cosine terms will add. That is not the case, however, since it is equivalent to saying that there is some

such that

,

where n and k are integers. That is, those students are assuming there is an

such that

, n and k integers.

Thus,

,

or

,

or

.

But if this is actually so, then as n and k are integers we would have π as the ratio of integers, i.e., π would be a rational number. Since 1761, however, π has been known to be irrational and so there are no integers n and k. And that means there is no

such that

, and so y_max(x) < 8.

Well, then, what is y_max(x)? Is it perhaps close to 8? You might try setting the derivative of y(x) to zero to find

, but that quickly leads to a mess...

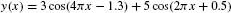
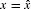
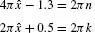
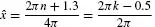
Table of contents

• Cover
• Title
• Copyright
• Contents
• Preface to the Paperback Edition
• Preface
• 1. Minimums, Maximums, Derivatives, and Computers
• 2. The First Extremal Problems
• 3. Medieval Maximization and Some Modern Twists
• 4. The Forgotten War of Descartes and Fermat
• 5. Calculus Steps Forward, Center Stage
• 6. Beyond Calculus
• 7. The Modern Age Begins
• Appendix A. The AM-GM Inequality
• Appendix B. The AM-QM Inequality, and Jensen's Inequality
• Appendix C. “The Sagacity of the Bees”
• Appendix D. Every Convex Figure Has a Perimeter Bisector
• Appendix E. The Gravitational Free-Fall Descent Time along a Circle
• Appendix F. The Area Enclosed by a Closed Curve
• Appendix G. Beltrami's Identity
• Appendix H. The Last Word on the Lost Fisherman Problem
• Appendix I. Solution to the New Challenge Problem
• Acknowledgments
• Index