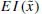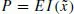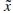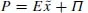Economic and Financial Decisions under Risk

Louis Eeckhoudt, Christian Gollier, Harris Schlesinger

• Publisher: Princeton University Press
• Year: 2011
• Print ISBN: 9780691122151, 9780691096551
• eBook ISBN: 9781400829217
• Topic: Economics
• Subtopic: Economic Theory
• Index: Economics

An understanding of risk and how to deal with it is an essential part of modern economics. Whether liability litigation for pharmaceutical firms or an individual's having insufficient wealth to retire, risk is something that can be recognized, quantified, analyzed, treated--and incorporated into our decision-making processes. This book represents a concise summary of basic multiperiod decision-making under risk. Its detailed coverage of a broad range of topics is ideally suited for use in advanced undergraduate and introductory graduate courses either as a self-contained text, or the introductory chapters combined with a selection of later chapters can represent core reading in courses on macroeconomics, insurance, portfolio choice, or asset pricing.


The authors start with the fundamentals of risk measurement and risk aversion. They then apply these concepts to insurance decisions and portfolio choice in a one-period model. After examining these decisions in their one-period setting, they devote most of the book to a multiperiod context, which adds the long-term perspective most risk management analyses require. Each chapter concludes with a discussion of the relevant literature and a set of problems.


The book presents a thoroughly accessible introduction to risk, bridging the gap between the traditionally separate economics and finance literatures.

Part II

Risk Management

3

Insurance Decisions

Insurance occurs when one party agrees to pay an indemnity to another party in case of the occurrence of a prespecified random event generating a loss for the initial risk-bearer. The most common example is an insurance policy, where the insurer is compensated by being paid a fixed premium by the policyholder. But many other contracts involve some form of insurance. For example, in share-cropping contracts, a landlord agrees to reduce the rent for his land in case of a low crop yield. In cost-plus contracts, a buyer agrees to pay a higher price if the producer incurs an unexpected increase in cost. In the case of income taxes, the state partially insures the losses of taxpayers by reducing the tax payment when incomes are low.

The shifting of risk is of considerable importance for the functioning of our modern economies.¹ Insurance allows for disentangling investment decisions from risk-taking decisions. Without it, we would certainly not have experienced the historical economic growth of the last century. Ford, Solvay, Rockefeller and others would not have taken the investment risks that they actually took without the possibility of sharing the risk with shareholders and insurers. Similarly, many consumers may not purchase new expensive cars or houses if they do not have a possibility of insuring them. Without an acceptable social net, young people would not engage in profitable but very risky investments in their human capital or in risky professional activities where their talents would most likely be recognized.

By pooling the risks of many policyholders, the insurer can take advantage of the Law of Large Numbers. So long as there is not much correlation between the insured risks of different policyholders, the insurer can diversify its risk. It is often convenient to think of the insurer as risk neutral: only the level of expected profits is what matters to the insurer. Indeed, the insurer might be thought of as a type of intermediary who collects and disperses funds amongst the policyholders. So in some sense, it is essentially the policyholders who are insuring one another. This concept is often referred to as the mutuality principle.

Insurance is a particular example of a type of risk-transfer strategy known as hedging. Hedging strategies typically involve entering into contracts whose payoffs are negatively related to one’s overall wealth or to one component of that wealth. Thus, for example, if wealth falls, the value of the contract rises, partially offsetting the loss in wealth. For instance, one might enter into contracts in the futures market to hedge against exchange-rate risk, when part of one’s income is in a foreign currency. Or one might use an option contract on the Standard and Poor (S&P) 500 Index to protect a pension fund against a precipitous fall in the value of stocks. Such options and futures contracts are typically based on financial-market data. Moreover, they contain various standardized attributes which make them fairly “liquid” assets, i.e. which allow them to be readily bought and sold in the market place. However, these hedging instruments typically entail another type of risk called a basis risk, which is a risk that the payoff does not offset losses exactly. For example, the value of one’s pension fund is not likely to be perfectly correlated with the S&P 500 Index, and hence index options will be an imperfect hedge.

Unlike these contracts, insurance is based on the level of one’s own individual loss rather than some index. Since there is no financial market for this unique loss, insurance contracts are not easily tradeable in secondary markets, and transaction costs are high. Even if a policyholder needed more insurance for her home, it would not help her to buy your homeowners’ insurance policy, since your policy will only pay when you have a loss, rather than when the policyholder has a loss. Thus, there is no secondary market for insurance contracts. In other words, compared to options and futures contracts, insurance is a rather “illiquid” asset. At the same time, insurance is a perfect hedge—the insurance indemnity is based on the occurrence of a prespecified loss. Insurance contracts do not contain the basis risk, which is prevalent in options and futures contacts.²

There is an added value to the policyholder from insurance because policyholders are risk-averse, that is they dislike risk on their wealth. Consider an individual facing a random loss

to her wealth, where

. An insurance contract stipulates a premium to be paid by the policyholder, P, and an indemnity schedule, I(x), which indicates the amount to be paid by the insurer for a loss of size x. There is full coverage if the insurer reimburses the policyholder for the full value of any loss, so that I(·) is the identity function, I(x) = x. The actuarial value of the contract is the expected indemnity

, which is the expected gross payoff from the insurance contract. The insurance premium is said to be actuarially fair (or often just “fair”) if it is equal to the actuarial value of the contract, i.e.

.

Table 3.1. Sempronius’s EU as a function of his insurance coverage I.

I	P	EU
0	0	86.395
1000	550	86.856
2000	1100	87.202
3000	1650	87.439
4000	2200	87.576
5000	2750	87.617
6000	3300	87.564
7000	3850	87.418
8000	4400	87.178

When the premium is fair, the expected net payoff on the insurance contract is zero. The purchase of a full insurance contract at an actuarially fair premium has the effect of replacing a random loss

by its expectation

. The private value of such a contract is equal to the value of the Arrow-Pratt risk premium attached to the risk

by the policyholder. Indeed, if we let Π denote this Arrow-Pratt risk premium, then the maximum premium the individual would be willing to pay for a full-coverage insurance policy is

. This maximum premium increases with the policyholder’s degree of risk a...

Table of contents

• Cover
• Title
• Copyright
• Contents
• Preface
• I    Decision Theory
• II    Risk Management
• III    Risk Sharing
• IV    Extensions
• Index