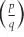The Best Writing on Mathematics 2012

Mircea Pitici

• Publisher: Princeton University Press
• Year: 2012
• Print ISBN: 9780691156552
• eBook ISBN: 9781400844678
• Topic: Mathematics
• Subtopic: Mathematics Essays
• Index: Mathematics

The year's finest writing on mathematics from around the world

This annual anthology brings together the year's finest mathematics writing from around the world. Featuring promising new voices alongside some of the foremost names in the field, The Best Writing on Mathematics 2012 makes available to a wide audience many articles not easily found anywhere else--and you don't need to be a mathematician to enjoy them. These writings offer surprising insights into the nature, meaning, and practice of mathematics today. They delve into the history, philosophy, teaching, and everyday occurrences of math, and take readers behind the scenes of today's hottest mathematical debates. Here Robert Lang explains mathematical aspects of origami foldings; Terence Tao discusses the frequency and distribution of the prime numbers; Timothy Gowers and Mario Livio ponder whether mathematics is invented or discovered; Brian Hayes describes what is special about a ball in five dimensions; Mark Colyvan glosses on the mathematics of dating; and much, much more.

In addition to presenting the year's most memorable writings on mathematics, this must-have anthology includes a foreword by esteemed mathematician David Mumford and an introduction by the editor Mircea Pitici. This book belongs on the shelf of anyone interested in where math has taken us--and where it is headed.

Was Cantor Surprised?

FERNANDO Q. GOUVÊA

Mathematicians love to tell each other stories. We tell them to our students, too, and they eventually pass them on. One of our favorites, and one that I heard as an undergraduate, is the story that Cantor was so surprised when he discovered one of his theorems that he said, “I see it, but I don’t believe it!” The suggestion was that sometimes we might have a proof, and therefore know that something is true, but nevertheless still find it hard to believe.

That sentence can be found in Cantor’s extended correspondence with Dedekind about ideas that he was just beginning to explore. This article argues that what Cantor meant to convey was not really surprise, or at least not the kind of surprise that is usually suggested. Rather, he was expressing a different, if equally familiar, emotion. To make this clear, we will look at Cantor’s sentence in the context of the correspondence as a whole.

Exercises in myth-busting are often unsuccessful. As Joel Brouwer says in his poem “A Library in Alexandria,”

… And so history gets written

to prove the legend is ridiculous. But soon the legend

replaces the history because the legend is more interesting.

Our only hope, then, lies in arguing not only that the standard story is false, but also that the real story is more interesting.

The Surprise

The result that supposedly surprised Cantor was the fact that sets of different dimension could have the same cardinality. Specifically, Cantor showed (of course, not yet using this language) that there was a bijection between the interval I = [0, 1] and the n-fold product I ⁿ = I × I × … × I.

There is no doubt, of course, that this result is “surprising,” i.e., that it is counterintuitive. In fact, Cantor said so explicitly, pointing out that he had expected something different. But the story has grown in the telling, and in particular Cantor’s phrase about seeing but not believing has been read as expressing what we usually mean when we see something happen and exclaim, “Unbelievable!” What we mean is not that we actually do not believe, but that we find what we know has happened to be hard to believe because it is so unusual, unexpected, surprising. In other words, the idea is that Cantor felt that the result was hard to believe even though he had a proof. His phrase has been read as suggesting that mathematical proof may engender rational certainty while still not creating intuitive certainty.

The story was then coopted to demonstrate that mathematicians often discover things that they did not expect or prove things that they did not actually want to prove. For example, here is William Byers [2, p. 179] in How Mathematicians Think:

Cantor himself initially believed that a higher-dimensional figure would have a larger cardinality than a lower-dimensional one. Even after he had found the argument that demonstrated that cardinality did not respect dimensions: that one-, two-, three-, even n-dimensional sets all had the same cardinality, he said, “I see it, but I don’t believe it.”

Did Cantor’s comment suggest that he found it hard to believe his own theorem even after he had proved it? Byers was by no means the first to say so.

Many mathematicians thinking about the experience of doing mathematics have found Cantor’s phrase useful. In his preface to the original (1937) publication of the Cantor-Dedekind correspondence, J. Cavaillès [14, p 3, my translation] already called attention to the phrase:

… these astonishing discoveries—astonishing first of all to the author himself: “I see it but I don’t believe it at all,”¹ he writes in 1877 to Dedekind about one of them—, these radically new notions …

Notice, however, that Cavaillès is still focused on the description of the result as “surprising” rather than on the issue of Cantor’s psychology. It was probably Jacques Hadamard who first connected the phrase to the question of how mathematicians think, and so in particular to what Cantor was thinking. In his famous Essay on the Psychology of Invention in the Mathematical Field, first published in 1945 [10, pp. 61–62] (only eight years after [14]), Hadamard is arguing about Newton’s ideas:

… if, strictly speaking, there could remain a doubt as to Newton’s example, others are completely beyond doubt. For instance, it is certain that Georg Cantor could not have foreseen a result of which he himself says “I see it, but I do not believe it.”.

Alas, when it comes to history, few things are “certain.”

The Main Characters

Our story plays out in the correspondence between Richard Dedekind and Georg Cantor during the 1870s. It is important to know something about each of them.

Richard Dedekind was born in Brunswick on October 6, 1831, and died in the same town, now part of Germany, on February 12, 1916. He studied at the University of Göttingen, where he was a contemporary and friend of Bernhard Riemann and where he heard Gauss lecture shortly before the old man’s death. After Gauss died, Lejeune Dirichlet came to Göttingen and became Dedekind’s friend and mentor.

Dedekind was a creative mathematician, but he was not particularly ambitious. He taught in Göttingen and in Zurich for a while, but in 1862 he returned to his hometown. There he taught at the local Polytechnikum, a provincial technical university. He lived with his brother and sister and seemed uninterested in offers to move to more prestigious institutions. See [1] for more on Dedekind’s life and work.

Our story begins in 1872. The first version of Dedekind’s ideal theory had appeared as Supplement X to Dirichlet’s Lectures in Number Theory (based on actual lectures by Dirichlet but entirely written by Dedekind). Also just published was one of his best known works, “Stetigkeit und irrationale Zahlen” (“Continuity and Irrational Numbers”; see [7]; an English translation is included in [5]). This work was his account of how to construct the real numbers as “cuts.” He had worked out the idea in 1858 but published it only 14 years later.

Georg Cantor was born in St. Petersburg, Russia, on March 3, 1845. He died in Halle, Germany, on January 6, 1918. He studied at the University of Berlin, where the mathematics department, led by Karl Weierstrass, Ernst Eduard Kummer, and Leopold Kronecker, might well have been the best in the world. His doctoral thesis was on the number theory of quadratic forms.

In 1869, Cantor moved to the University of Halle and shifted his interests to the study of the convergence of trigonometric series. Very much under Weierstrass’s influence, he too introduced a way to construct the real numbers, using what he called “fundamental series.” (We call them “Cauchy sequences.”) His paper on this construction also appeared in 1872.

Cantor’s lifelong dream seems to have been to return to Berlin as a professor, but it never happened. He rose through the ranks in Halle, becoming a full professor in 1879 and staying there until his death. See [13] for a short account of Cantor’s life. The standard account of Cantor’s mathematical work is [4].

Cantor is best known, of course, for the creation of set theory, and in particular for his theory of transfinite cardinals and ordinals. When our story begins, this work was mostly still in the future. In fact, the birth of several of these ideas can be observed in the correspondence with Dedekind. This correspondence was first published in [14]; we quote it from the English translation by William Ewald in [8, pp 843–878].

“Allow Me to Put a Question to You”

Dedekind and Cantor met in Switzerland when they were both on vacation there. Cantor had sent Dedekind a copy of the paper containing his construction of the real numbers. Dedekind responded, of course, by sending Cantor a copy of his booklet. And so begins the story.

Cantor was 27 years old and very much a beginner, while Dedekind was 41 and at the height of his powers; this difference accounts for the tone of deference on Cantor’s side of the correspondence. Cantor’s first letter acknowledged receipt of [7] and says that “my conception [of the real numbers] agrees entirely with yours,” the only difference being in the actual construction. But on November 29, 1873, Cantor moves on to new ideas:

Allow me to put a question to you. It has a certain theoretical interest for me, but I cannot answer it myself; perhaps you can, and would be so good as to write me about it. It is as follows.

Take the totality of all positive whole-numbered individuals n and denote it by (n). And imagine, say, the totality of all positive real numerical quantities x and designate it by (x). The question is simply, Can (n) be correlated to (x) in such a way that to each individual of the one totality there corresponds one and only one of the other? At first glance one says to oneself no, it is not possible, for (n) consists of discrete parts while (x) forms a continuum. But nothing is gained by this objection, and although I incline to the view that (n) and (x) permit no one-to-one correlation, I cannot find the explanation which I seek; perhaps it is very easy.

In the next few lines, Cantor points out that the question is not as dumb as it looks, since “the totality

of all positive rational numbers” can be put in one-to-one correspondence with the integers.

We do not have Dedekind’s side of the correspondence, but his notes indicate that he responded indicating that (1) he could not answer the question either, (2) he could show that the set of all algebraic numbers is countable, and (3) he didn’t think the question was all that interesting. Cantor responded on December 2:

I was exceptionally pleased to receive your answer to my last letter. I put my question to you because I had wondered about it already several years ago, and was never certain whether the difficulty I found was subjective or whether it was inherent in the subject. Since you write that you too are unable to answer it, I may assume the latter.—In addition, I should like to add that I have never seriously occupied myself with it, because it has no special practical interest for me. And I entirely agree with you when you say that for this reason it does not deserve much effo...

Table of contents

• Cover
• Title Page
• Copyright
• Dedication
• Contents
• Foreword: The Synergy of Pure and Applied Mathematics, of the Abstract and the Concrete
• Introduction
• Why Math Works
• Is Mathematics Discovered or Invented?
• The Unplanned Impact of Mathematics
• An Adventure in the Nth Dimension
• Structure and Randomness in the Prime Numbers
• The Strangest Numbers in String Theory
• Mathematics Meets Photography: The Viewable Sphere
• Dancing Mathematics and the Mathematics of Dance
• Can One Hear the Sound of a Theorem?
• Flat-Unfoldability and Woven Origami Tessellations
• A Continuous Path from High School Calculus to University Analysis
• Mathematics Teachers’ Subtle, Complex Disciplinary Knowledge
• How to Be a Good Teacher Is an Undecidable Problem
• How Your Philosophy of Mathematics Impacts Your Teaching
• Variables in Mathematics Education
• Bottom Line on Mathematics Education
• History of Mathematics and History of Science Reunited?
• Augustus De Morgan behind the Scenes
• Routing Problems: A Historical Perspective
• The Cycloid and Jean Bernoulli
• Was Cantor Surprised?
• Why Is There Philosophy of Mathematics at All?
• Ultimate Logic: To Infinity and Beyond
• Mating, Dating, and Mathematics: It’s All in the Game
• Contributors
• Notable Texts
• Acknowledgments
• Credits