Mathematical Tools for Understanding Infectious Disease Dynamics

Odo Diekmann, Hans Heesterbeek, Tom Britton

• Publisher: Princeton University Press
• Year: 2012
• Print ISBN: 9780691155395
• eBook ISBN: 9781400845620
• Topic: Biological Sciences
• Subtopic: Applied Mathematics
• Index: Biological Sciences

Mathematical modeling is critical to our understanding of how infectious diseases spread at the individual and population levels. This book gives readers the necessary skills to correctly formulate and analyze mathematical models in infectious disease epidemiology, and is the first treatment of the subject to integrate deterministic and stochastic models and methods.

Mathematical Tools for Understanding Infectious Disease Dynamics fully explains how to translate biological assumptions into mathematics to construct useful and consistent models, and how to use the biological interpretation and mathematical reasoning to analyze these models. It shows how to relate models to data through statistical inference, and how to gain important insights into infectious disease dynamics by translating mathematical results back to biology. This comprehensive and accessible book also features numerous detailed exercises throughout; full elaborations to all exercises are provided.

• Covers the latest research in mathematical modeling of infectious disease epidemiology
• Integrates deterministic and stochastic approaches
• Teaches skills in model construction, analysis, inference, and interpretation
• Features numerous exercises and their detailed elaborations
• Motivated by real-world applications throughout

Part IV

Elaborations

Chapter Sixteen

Elaborations for Part I

16.1 ELABORATIONS FOR CHAPTER 1

Exercise 1.1 Let c denote the number of blood meals a mosquito takes per unit of time. Suppose a human receives k bites per unit of time. Consistency requires that kD_human = cD_mosquito. Our assumption is that c is a given constant. Hence necessarily

Exercise 1.2 cT_mp_m.

Exercise 1.3 kT_hp_h.

Exercise 1.4 Consider one infected mosquito. It is expected to infect cT_mp_m humans, each of which is expected to infect kT_hp_h mosquitoes. So, going full circle, we have a multiplication factor

When this multiplication factor is below one, an initial infection will die out in a small number of ‘generations.’ If, however, it is above one then most likely (see Section 1.2.2 for a qualitative and quantitative elaboration of how likely this actually is) an avalanche will result.

Exercise 1.5 i) R₀ = q₁ + 2_q2. Using q₀ + q₁ + q₂ = 1 we can rewrite this as R₀ = 1 + q₂ − q₀. If follows that R₀ > 1 if q₂ > q₀, and that R₀ ≤ 1 if q₂ ≤ q₀.

ii) Individuals are indistinguishable, so for each the probability that its line of descent will stop equals z. By independence, the probability that both lines stop then equals z².

iii) Consider one individual. If this individual has no offspring, its line of descent will stop with certainty. If it produces one offspring, its line of descent will stop with probability z. If it produces two offspring, its line of descent will stop with probability z². Hence consistency requires that

z = q₀1 + q₁z + q₂z².

iv) If we substitute q₁ = 1 − q₀ − q₂ we obtain z = q₀ + z − q₀z − q₂z + q₂z² and next q₀(z − 1) = q₂z(z − 1). From this we see that either z = 1 or that q₀ = q₂z.

v) We recall from i) that R₀ ≤ 1 corresponds to q₂ ≤ q₀ and hence to q₀/q₂ ≥ 1. As z should be a probability, we conclude that only the possibility z = 1 remains.

vi) If R₀ > 1 then q₂ > q₀ so q₀q₂ < 1. We expect that in this case z = q₀q₂ and that with complementary probability 1 − z > 0 the line of descent of the individual will grow exponentially.

Exercise 1.6 i) Direct substitution.

ii) g(1) =

and, since {q_k} should be a probability distribution, we require that

.

iii) By term-by-term differentiation, g′(z) =

and therefore g′(1) =

iv) All q_k ≥ 0 (by their interpretation) and

guarantee that at least one of the q_k is strictly positive; the expression for g′(z) derived in 1.6-iii then implies g′(z) > 0, provided that q₀ < 1.

v) g″(z) =

, and the argument is now identical to that used in proving 1.6-iv. Note that if q₀ + q₁ = 1 then g″(z) = 0. The strict inequality g″(z) ...

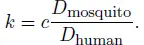
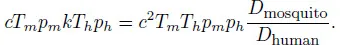
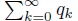
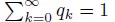
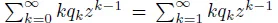
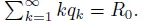
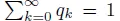
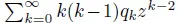
Table of contents

• Cover
• Title
• Copyright
• Contents
• Preface
• I The bare bones: Basic issues in the simplest context
• II Structured populations
• III Case studies on inference
• IV Elaborations
• Bibliography
• Index