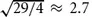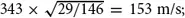Why You Hear What You Hear

An Experiential Approach to Sound, Music, and Psychoacoustics

Eric J. Heller

• Publisher: Princeton University Press
• Year: 2012
• ISBN:
  9781400845583
• Topic: Scienze fisiche
• Subtopic: Fisica

A groundbreaking textbook that explores the phenomena and physics of music and sound Why You Hear What You Hear is the first book on the physics of sound for the nonspecialist to empower readers with a hands-on, ears-open approach that includes production, analysis, and perception of sound. The book makes possible a deep intuitive understanding of many aspects of sound, as opposed to the usual approach of mere description. This goal is aided by hundreds of original illustrations and examples, many of which the reader can reproduce and adjust using the same tools used by the author (e.g., very accessible applets for PC and Mac, and interactive web-based examples, simulations, and analysis tools that can be found on the book's website: whyyouhearwhatyouhear.com). Readers are positioned to build intuition by participating in discovery.This truly progressive introduction to sound engages and informs amateur and professional musicians, performers, teachers, sound engineers, students of many stripes, and indeed anyone interested in the auditory world. The book does not hesitate to follow entertaining and sometimes controversial side trips into the history and world of acoustics, reinforcing key concepts. You will discover how musical instruments really work, how pitch is perceived, and how sound can be amplified with no external power source.Sound is key to our lives, and is the most accessible portal to the vibratory universe. This book takes you there.

• The first book on sound to offer interactive tools, building conceptual understanding via an experiential approach
• Supplementary website (http://www.whyyouhearwhatyouhear.com) provides Java, MAX, and other free, multiplatform, interactive graphical and sound applets
• Extensive selection of original exercises available on the web with solutions
• Nearly 400 full-color illustrations, many of simulations that students can do

I Sound Itself

1 How Sound Propagates

Sound takes place when bodies strike the air, … by its being moved in a corresponding manner; the air being contracted and expanded and overtaken, and again struck by the impulses of the breath and the strings, for when air falls upon and strikes the air which is next to it, the air is carried forward with an impetus, and that which is contiguous to the first is carried onward; so that the same voice spreads every way as far as the motion of the air takes place.

—Aristotle (384–322 BCE), Treatise on Sound and Hearing

More than two thousand years ago, Aristotle correctly declared that sound consists of the propagation of air pressure variations.

Even to the casual observer, sound is plainly revealed to be a consequence of vibrating or pulsating objects in contact with air. Surfaces feel a force from all the molecules colliding with them; every molecule bouncing off the surface gives it a tiny shove. A bounce is a change of velocity and thus an acceleration, imparting a force F on the molecule (and an equal and opposite force acting on the surface) according to Sir Isaac Newton’s law F = ma, where m is the mass of the accelerated molecule, and a is the acceleration.

Fluctuations of pressure above (condensations) and below (rarefactions) the average pressure, arriving at the surface as sound, cause a very small increase or decrease in the number of collisions per second, and a corresponding tiny but measurable change of force on the surface. These fluctuations above and below the ambient pressure are called the pressure amplitude δP, where the total pressure is P = P₀ + δP, and P₀ is the ambient pressure. Usually only the amplitudes matter to us; it is changes in pressure that we hear, not the ambient pressure. We (and other animals) however are spectacularly sensitive to these changes; a pressure fluctuation of just a few parts in a billion (a few billionths of an atmosphere) is enough for us to hear if it happens fast enough.

As small as it is, the tympanum is huge on the molecular scale. There are so many molecules colliding with it every millisecond (roughly 10²³—that’s 1 followed by 23 zeros) that they average out and give a nearly steady pressure, amounting to about 14 lb of force on every square inch. Air pressure is usually measured in kilopascals (1 kPa = 0.145 pounds per square inch, or psi). Sea-level air pressure is about 100 kPa, or 14.5 psi. The tympanum membrane, which separates the middle and outer ear, normally has equal air pressure on both sides, so there is no net force on it, except for tiny fluctuations.

Aristotle could not have known that air is a seething mass of molecules crashing into one another. More than a billion collisions are suffered by every molecule every second at sea level and room temperature. In spite of all the collisions, air is mostly empty space: the molecules occupy only about one part in 5000 of the available volume. Think of 10 bumper cars in an area the size of a football field. You might think that this was a relatively safe, low density of cars—unless each car was traveling at thousands of kilometers per hour. There would be many collisions every second. Between collisions, molecules speed along a straight path at typically half a kilometer per second, managing to travel only a tenth of the length of a typical bacterium before suffering another collision.

The density and speed of air molecules are in this way sufficient to explain atmospheric air pressure and the speed of sound. Individually, the air molecules (mostly diatomic nitrogen and oxygen) act like drunken messengers flying and colliding every which way. Nonetheless, these collisions can collectively communicate even slight fluctuations in pressure to neighboring collections of molecules, which in turn pass them on to their neighbors, leading to sound propagation. Air molecules are usually not traveling directly along the path of the sound wave; the information that there is higher or lower pressure somewhere propagates no faster than the average speed of molecules along a given direction.

The typical 500 meter/second (m/s) molecule is traveling either in the wrong direction or only 300 to 400 m/s along the direction of propagation of the sound. Thus the effective speed with which the morass of molecules communicates pressure variations is less than their average speed of 500 m/s. The measured speed of sound in air is about 343 m/s at room temperature.

The “seething mass of molecules” picture explains why the speed of sound is insensitive to pressure, since pressure hardly affects the speed of individual molecules. They crash into each other more often at high pressure, but between collisions they travel at a speed that depends only on the temperature, not the pressure. The speed of sound on Mount Everest is nearly the same as at sea level, if the temperatures are the same.

The average speed of molecules is proportional to the square root of the temperature, and inversely proportional to the square root of the mass of the molecules in the gas.

“Helium voice,” the Donald Duck-like sound when someone speaking has just inhaled a puff of helium, is the result of the much higher speed of sound in helium than in air. Helium has a mass of four atomic units; air has an average mass of about 29 atomic units and

. The speed of sound in helium, 972 m/s, is about 2.8 times that of air, at 343 m/s. Another harmless gas (except that like helium, it displaces oxygen and can be lethal if breathed for more than a short time), sulfur hexaflouride, SF₆, is much heavier at 146 atomic units and should have a speed of

the measured value is 150, less than half the speed of sound in air. “SF₆ voice” is even more astonishing in its effect than helium voice, and in the opposite direction. (However, the nature of and reasons for the changes in the sound of the voice using helium and SF₆ will be explained in section 17.9. In spite of impressions, the gases do not change the pitch of the voice!)

The energy needed to make audible sound is very small. You can shout for a year, and the energy produced that winds up as sound would not be enough to boil a cup of water. A full orchestra playing loudly produces only about enough sound energy to power a weak lightbulb. An orchestral crescendo might bathe a listener in sound pressure fluctuations of about 1 pascal (1 Pa). Sea-level air pressure is 100,000 Pa, so the crescendo loud enough to damage your hearing, if it lingered too long, is varying the pressure by just 0.001%. Clearly, a very delicate detection system is at work. We will find in chapter 21 that human hearing depends on a few thousand single-molecule links between cochlear hair cells.

At the extreme—loud sound near the threshold of pain—the air pressure variations are over a million times bigger than the threshold of hearing, or about a 0.03% pressure variation, 30 Pa or so. This still seems small, and yet is almost immediately damaging! This sound level corresponds to a power arriving at the ear 10,000,000,000,000 (10¹³) times larger than that which produces the softest sound we can hear. (The power increases as the square of the pressure variations.) The dynamic range of our hearing is truly remarkable.

Why should you buy a 600-watt (W) amplifier for your loudspeakers if a full orchestra normally produces just a watt of power, 40 or 50 W at the loudest? The answer is that to reproduce sound, rather large forces must be exerted on the speaker cone to get it to vibrate in a prescribed way. The conversion efficiency from motion of a loudspeaker cone to sound is very low. The cones are moved with electric currents in coils near magnets, wasting considerable energy. Imagine all the effort you would expend waving your hands back and forth 1000 times. Only a tiny fraction of that energy would go into pushing air around; most of the energy expended would go into working against yourself, so to speak: internal friction, stopping your arms with one set of muscles after starting them swinging with another, working against gravity, and so on. So it is with a loudspeaker. For that matter, musicians can work up a sweat playing an instrument, all to produce well under a tenth of a watt of sound.

1.1 Push and Pushback: Impedance

We need to develop a better intuitive foundation for sound propagation. The “drunken messenger” picture explains the speed of sound but applies on the molecular scale, too small to give a good sense of wave phenomena such as reflection, diffraction, refraction, and so on. For example, much of the sound traveling down a tube reflects from its open end, reversing direction rather than exiting to freedom. Why doesn’t the sound just leave the tube? Why is the reflected wave a rarefaction (pressure low relative to ambient) if the incident wave approaching the end of the tube was a compression (pressure high relative to ambient)? Why does sound of high-enough frequency (the frequency is the number of wave crests traveling by per second), on the other hand, mostly escape the tube without reflecting? There are not many references that provide a foundation for a comprehensive understanding of these sorts of phenomena; those written for engineers and physicists all too often derive equations and formulas but skimp on the intuition.

Imagine dividing air into small cells. Each cell is large on the molecular scale; they are packed one next to the other. The size of the cell is determined by the wavelength of the sound involved (there needs to be at least several cells per wavelength) and the details of any obstacles, sound sources, and so on. If we can understand how the cells communicate with each other, are pushed by and then push back on neighboring cells, we can understand propagation, reflection, diffraction, and even refraction of sound. This is our first glance at a powerful engineer’s trick, wherein the properties of complex objects are lumped into a few well-chosen summarizing properties. These have vastly less information than the original system, but enough to carry the essential physics, and lead more easily to the correct conclusions.

To understand impedance in air, we begin by considering solid elastic bodies, such as pucks on an air hockey table or coins on a slick surface. We need to understand such things in any case, because usually before air is set in motion, something more massive, like a string or a block of wood, is set in motion. Each puck or coin is a lumped object—we ignore the details of atomic or molecular structure inside, but keep essentials such as size, density, and elasticity, just as we will for air cells when we return t...