Introduction to Modeling Convection in Planets and Stars

Magnetic Field, Density Stratification, Rotation

Gary A. Glatzmaier

• Publisher: Princeton University Press
• Year: 2013
• Print ISBN: 9780691141732, 9780691141725
• eBook ISBN: 9781400848904
• Topic: Physical Sciences
• Subtopic: Data Modelling & Design

This book provides readers with the skills they need to write computer codes that simulate convection, internal gravity waves, and magnetic field generation in the interiors and atmospheres of rotating planets and stars. Using a teaching method perfected in the classroom, Gary Glatzmaier begins by offering a step-by-step guide on how to design codes for simulating nonlinear time-dependent thermal convection in a two-dimensional box using Fourier expansions in the horizontal direction and finite differences in the vertical direction. He then describes how to implement more efficient and accurate numerical methods and more realistic geometries in two and three dimensions. In the third part of the book, Glatzmaier demonstrates how to incorporate more sophisticated physics, including the effects of magnetic field, density stratification, and rotation.


Featuring numerous exercises throughout, this is an ideal textbook for students and an essential resource for researchers.

• Describes how to create codes that simulate the internal dynamics of planets and stars


• Builds on basic concepts and simple methods


• Shows how to improve the efficiency and accuracy of the numerical methods


• Describes more relevant geometries and boundary conditions


• Demonstrates how to incorporate more sophisticated physics

PART 1

The Fundamentals

Chapter One

A Model of Rayleigh-Bénard Convection

There are two basic types of fluid flows within planets and stars that are driven by thermally produced buoyancy forces: thermal convection and internal gravity waves. The type depends on the thermal stratification within the fluid region. The Earth’s atmosphere and ocean, for example, are in most places convectively stable, which means that they support internal gravity waves, not (usually) convection (but see Chapter 7). On warm afternoons, however, the sun can heat the ground surface, which changes the vertical temperature gradient in the troposphere and makes the atmosphere convectively unstable; the appearance of cumulus clouds is an indication of the resulting convective heat (and moisture) flux. Thermal convection likely also occurs in the Earth’s liquid outer core, which generates the geomagnetic field, and, on a much longer time scale, in the Earth’s mantle, which drives plate tectonics and, on a much shorter time scale, initiates earthquakes and volcanic eruptions. Thermal convection is seen on the surface of the sun and likely occurs in the outer 30% of the solar radius, where solar magnetic field is generated. Below this depth buoyancy likely drives internal gravity waves. Rotation strongly influences the style of the convection and waves in all of these examples except the mantle, which is dominated by viscous forces.

Computer simulation studies, over the past few decades, have significantly improved our understanding of these phenomena. Some studies, like those for the atmospheres of the Earth and sun, have provided physical explanations and predictions of the observations. Others, like those for the deep interiors of the Earth and sun, have provided detailed theories and predictions of the dynamics that cannot be directly observed. As computers continue to improve in speed and memory, computer programs are able to run at greater spatial and temporal resolutions, which improves the quality of and confidence in the simulations. Numerical and programming methods have also improved and need to continue to improve to take full advantage of the improvements in computer hardware.

1.1 BASIC THEORY

We begin with a simple description of the fundamental dynamics expected in a fluid that is convectively stable and in one that is convectively unstable. Then we review the equations that govern fluid dynamics based on conservation of mass, momentum, and energy.

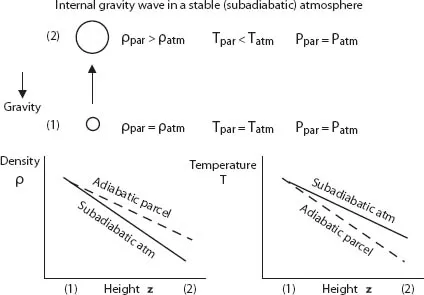
Figure 1.1 A schematic of a test parcel that is raised adiabatically from position (1) to position (2) in an atmosphere that has subadiabatic temperature and density stratifications.

1.1.1 Thermal Convection and Internal Gravity Waves

The thermal stability of a fluid within a gravitational field is determined by its horizontal-mean (i.e., ambient) vertical temperature gradient. The classic way of describing this is to consider a fluid in hydrostatic equilibrium, i.e., the weight of the fluid above a given height (per cross-sectional area) is supported by the pressure at that height. Therefore, the vertical pressure gradient is negative. (As usual, “vertical” here and throughout this book refers to the direction of increasing height or radius, opposite to that of the gravitational acceleration.) In the interiors of planets and stars the horizontal-mean density and temperature also decrease with height. The question is how does the vertical temperature gradient of this fluid (atmosphere) compare with what an adiabatic temperature gradient would be.

Consider a small (test) parcel of fluid (Fig. 1.1) that, at its initial position (1), has the same pressure, density, and temperature as the surrounding atmosphere at that position. Imagine raising the parcel to a new height (2), fast enough so there is no heat transfer between it and the surrounding atmosphere but slowly enough that it remains in pressure equilibrium with its surroundings; that is, its upward velocity is much less than the local sound speed. Assuming this process is reversible and also adiabatic since there is no heat transfer, the parcel’s entropy remains constant while rising; that is, this is an isentropic process. However, since it remains in pressure equilibrium with the surroundings, its density and temperature both decrease as it rises because the decrease in pressure causes it to expand. If, when reaching its new higher position (2), its temperature has decreased more than the temperature of the surrounding atmosphere has decreased over that change in height, its density there will be greater than the density of the surrounding atmosphere there (assuming a typical coefficient of thermal expansion). Therefore, the parcel will be antibuoyant and, when no longer externally supported, will fall. As the parcel falls its temperature increases faster than the surrounding temperature and when it passes the initial position its temperature exceeds the temperature of surrounding atmosphere, causing the now buoyant parcel to eventually stop falling and then to start rising. This process of accelerating downward when it is above the initial position and accelerating upward when below the initial position is called an internal gravity wave and the surrounding atmosphere is said to be convectively stable. Recall that this occurs when the surrounding temperature decreases less rapidly with height than an adiabatic temperature profile would, since the test parcel moves adiabatically. That is, the surrounding temperature gradient is subadiabatic. The temperature stratification would be extremely stable if the surrounding temperature increased with height. In reality, thermal and viscous diffusion cause internal gravity waves to decay with time unless they are continually being excited.

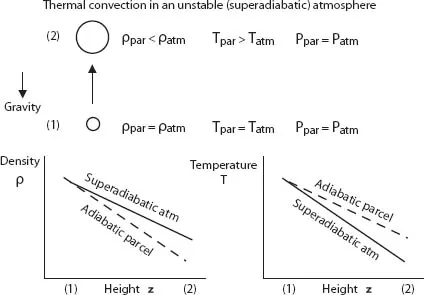
Figure 1.2 A schematic of a test parcel that is raised adiabatically from position (1) to position (2) in an atmosphere that has superadiabatic temperature and density stratifications.

Now consider the case for which the changes in the parcel’s temperature as it moves up and down are less than that of the surrounding atmosphere (Fig. 1.2). That is, consider a surrounding atmosphere with a superadiabatic temperature gradient. In this case, when reaching its new higher position (2), the parcel’s temperature will be higher than the temperature of the surroundings there and so its density will be less than that of the surroundings. This makes the parcel buoyant and so, when no longer externally supported, it continues to rise. Likewise, if the parcel were initially lowered, it would continue to sink. Typically, a rising parcel will eventually encounter a cold impermeable top boundary where it gives up heat by conduction, contracts, and becomes antibuoyant. This causes it to fall until it encounters a hot impermeable botto...

Table of contents

• Cover
• Title Page
• Copyright Page
• Dedication Page
• Contents
• Preface
• Part I. The Fundamentals
• Color insert
• Part II. Additional Numerical Methods
• Part III. Additional Physics
• Appendix A A Tridiagonal Matrix Solver
• Appendix B Making Computer-Graphical Movies
• Appendix C Legendre Functions and Gaussian Quadrature
• Appendix D Parallel Processing: OpenMP
• Appendix E Parallel Processing: MPI
• Bibliography
• Index