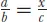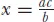Taming the Unknown

A History of Algebra from Antiquity to the Early Twentieth Century

Victor J. Katz, Karen Hunger Parshall

• Publisher: Princeton University Press
• Year: 2014
• ISBN:
  9781400850525
• Topic: Matemáticas
• Subtopic: Historia y filosofía de las matemáticas

What is algebra? For some, it is an abstract language of x's and y's. For mathematics majors and professional mathematicians, it is a world of axiomatically defined constructs like groups, rings, and fields. Taming the Unknown considers how these two seemingly different types of algebra evolved and how they relate. Victor Katz and Karen Parshall explore the history of algebra, from its roots in the ancient civilizations of Egypt, Mesopotamia, Greece, China, and India, through its development in the medieval Islamic world and medieval and early modern Europe, to its modern form in the early twentieth century.Defining algebra originally as a collection of techniques for determining unknowns, the authors trace the development of these techniques from geometric beginnings in ancient Egypt and Mesopotamia and classical Greece. They show how similar problems were tackled in Alexandrian Greece, in China, and in India, then look at how medieval Islamic scholars shifted to an algorithmic stage, which was further developed by medieval and early modern European mathematicians. With the introduction of a flexible and operative symbolism in the sixteenth and seventeenth centuries, algebra entered into a dynamic period characterized by the analytic geometry that could evaluate curves represented by equations in two variables, thereby solving problems in the physics of motion. This new symbolism freed mathematicians to study equations of degrees higher than two and three, ultimately leading to the present abstract era. Taming the Unknown follows algebra's remarkable growth through different epochs around the globe.

1

Prelude: What Is Algebra?

What is algebra? It is a question to which a high school student will give one answer, a college student majoring in mathematics another, and a professor who teaches graduate courses and conducts algebraic research a third. The educated “layperson,” on the other hand, might simply grimace while retorting, “Oh, I never did well in mathematics. Wasn’t algebra all of that x and y stuff that I could never figure out?” This ostensibly simple question, then, apparently has a number of possible answers. What do the “experts” say?

On 18 April 2006, the National Mathematics Advisory Panel (NMAP) within the US Department of Education was established by executive order of then President George W. Bush to advise him, as well as the Secretary of Education, on means to “foster greater knowledge of and improved performance in mathematics among American students.”¹ Among the panel’s charges was to make recommendations on “the critical skills and skill progressions for students to acquire competence in algebra and readiness for higher levels of mathematics.” Why should competence in algebra have been especially singled out?

When it issued its final report in March 2008, the panel stated that “a strong grounding in high school mathematics through Algebra II or higher correlates powerfully with access to college, graduation from college, and earning in the top quartile of income from employment.”² Furthermore, it acknowledged that “although our students encounter difficulties with many aspects of mathematics, many observers of educational policy see Algebra as a central concern.” The panel had thus sought to determine how best to prepare students for entry into algebra and, since algebra was of such concern, it had first to come to terms with the question, what is the essential content of school algebra? In answer, it identified the following as the major topics: symbols and expressions, linear equations, quadratic equations, functions, the algebra of polynomials, and combinatorics and finite probability. Of course, each of these topics encompasses several subtopics. For example, the “algebra of polynomials” includes complex numbers and operations, the fundamental theorem of algebra, and Pascal’s triangle. Interestingly, the panel mentioned “logarithmic functions” and “trigonometric functions” under the topic of “functions” but made no explicit mention of analytic geometry except in the special case of graphs of quadratic functions. Although the details of the panel’s list might prompt these and other quibbles, it nevertheless gives some idea of what high school students, in the United States at least, generally study—or should study—under the rubric of “algebra.”

These topics, however, constitute “school algebra.” What about algebra at the college level? Most courses entitled “college algebra” in the United States simply revisit the aforementioned topics, sometimes going into slightly greater depth than is expected in high school. Courses for mathematics majors—entitled “modern algebra” or “abstract algebra”—are quite another matter, however. They embrace totally different topics: groups, rings, fields, and, often, Galois theory. Sometimes such courses also include vectors, matrices, determinants, and algebras (where the latter is a technical term quite different from the broad subject under consideration here).

And then there is algebra at the graduate and research levels. Graduate students may take courses in commutative or noncommutative algebra, representation theory, or Lie theory, while research mathematicians styled “algebraists” may deal with topics like “homological functors on modules,” “algebraic coding theory,” “regular local rings,” or any one of hundreds of topics listed in the American Mathematical Society’s “Mathematics Subject Classification.” How do all of these subjects at all of these levels of sophistication fit together to constitute something called “algebra”? Before addressing this question, we might first ask why we need this book about it?

WHY THIS BOOK?

To be sure, the historical literature already includes several more or less widely ranging books on the history of algebra that are targeted, like the present book, at those with a background equivalent to a college major in mathematics;³ a recent “popular” book assumes even less in the way of mathematical prerequisites.⁴ Most in the former group, however, are limited either in the eras covered or in geographical reach, while that in the latter has too many errors of fact and interpretation to stand unchallenged. This book thus grew out of a shared realization that the time was ripe for a history of algebra that told the broader story by incorporating new scholarship on the diverse regions within which algebraic thought developed and by tracing the major themes into the early twentieth century with the advent of the so-called “modern algebra.”

We also believe that this is a story very much worth telling, since it is a history very much worth knowing. Using the history of algebra, teachers of the subject, either at the school or at the college level, can increase students’ overall understanding of the material. The “logical” development so prevalent in our textbooks is often sterile because it explains neither why people were interested in a particular algebraic topic in the first place nor why our students should be interested in that topic today. History, on the other hand, often demonstrates the reasons for both. With an understanding of the historical development of algebra, moreover, teachers can better impart to their students an appreciation that algebra is not arbitrary, that it is not created “full-blown” by fiat. Rather, it develops at the hands of people who need to solve vital problems, problems the solutions of which merit understanding. Algebra has been and is being created in many areas of the world, with the same solution often appearing in disparate times and places.

And this is neither a story nor a history limited to school students and their teachers. College-level mathematics students and their professors should also know the roots of the algebra they study. With an understanding of the historical development of the field, professors can stimulate their students to master often complex notions by motivating the material through the historical questions that prompted its development. In absorbing the idea, moreover, that people struggled with many important mathematical ideas before finding their solutions, that they frequently could not solve problems entirely, and that they consciously left them for their successors to explore, students can better appreciate the mathematical endeavor and its shared purpose. To paraphrase the great seventeenth- and early eighteenth-century English mathematician and natural philosopher, Sir Isaac Newton, mathematicians have always seen farther by “standing on the shoulders” of those who came before them.

One of our goals in the present book is thus to show how—in often convoluted historical twists and turns—the deeper and deeper consideration of some of the earliest algebraic topics—those generally covered in schools—ultimately led mathematicians to discover or invent the ideas that constitute much of the algebra studied by advanced college-level students. And, although the prerequisites assumed of our readers limit our exploration of the development of the more advanced algebraic topics encountered at the graduate and research levels, we provide at least a glimpse of the origins of some of those more advanced topics in the book’s final chapters.

SETTING AND EXAMINING THE HISTORICAL PARAMETERS

Nearly five decades before the National Mathematics Advisory Panel issued its report, historian of mathematics, Michael Mahoney, gave a more abstract definition of algebra, or, as he termed it, the “algebraic mode of thought”:

What should be understood as the “algebraic mode of thought”? It has three main characteristics: first, this mode of thought is characterized by the use of an operative symbolism, that is, a symbolism that not only abbreviates words but represents the workings of the combinatory operations, or, in other words, a symbolism with which one operates. Second, precisely because of the central role of combinatory operations, the algebraic mode of thought deals with mathematical relations rather than objects. Third, the algebraic mode of thought is free of ontological commitment…. In particular, this mode of thought is free of the intuitive ontology of the physical world. Concepts like “space,” “dimension,” and even “number” are understood in a purely mathematical sense, without reference to their physical interpretation.⁵

Interestingly, Mahoney’s first characteristic of algebraic thought as an “operative symbolism”—as well as the discussion of symbolism—is the first of the topics mentioned in the NMAP report. If, however, we believed that an operative symbolism is a necessary characteristic of algebra, this book would not begin before the seventeenth century since, before that time, mathematics was generally carried out in words. Here, we shall argue that symbolism is not necessary for algebra, although it has certainly come to characterize it—and, indeed, all of mathematics—over the past three centuries. We shall also argue that, initially, algebra dealt with objects rather than relations and that the beginnings of algebra actually required physical interpretations.

The roots of algebra go back thousands of years, as we shall see in the next chapter, but the two earliest texts that serve to define a subject of algebra are the Arithmetica of Diophantus (third century CE) and The Compendious Book on the Calculation of al-Jabr and al-Muqābala of al-Khwārizmī (ninth century CE). Although neither of these books required physical interpretations of the problems they presented, they did deal with objects rather than relations and neither used any operative symbolism. However, as we shall see below, al-Khwārizmī’s book in particular was on the cusp of the change from “physical interpretations” to “abstract number” in the development of algebra. And, although the term “algebra” is absent from the texts both of Diophantus and al-Khwārizmī, it is clear that their major goal was to find unknown numbers that were determined by their relationship to already known numbers, that is, in modern terminology, to solve equations. This is also one of the goals listed in the NMAP report, so it would be difficult to deny that these works exhibit “algebraic thought.” Thus, in order to study algebra historically, we need a definition of it somewhat different from that of Mahoney, which applies only to the algebra of the past three centuries.

It is interesting that school algebra texts today do not even attempt to define their subject. In the eighteenth and nineteenth centuries, however, textbook writers had no such compunction. The standard definition, in fact, was one given by Leonhard Euler in his 1770 textbook, Elements of Algebra. Algebra, for Euler, was “the science which teaches how to determine unknown quantities by means of those that are known.”⁶ He thus articulated explicitly what most of his predecessors had implicitly taken as the meaning of their subject, and we follow his lead here in adopting his definition, at least in the initial stages of this book when we explore how “determining unknowns” was accomplished in different times and places.

Now, there is no denying that, taken literally, Euler’s definition of algebra is vague. It is, for example, not immediately clear what constitutes the “quantity” to be determined. Certainly, a “number” is a quantity—however one may define “number”—but is a line segment a “quantity”? Is a vector? Euler was actually clear on this point. “In algebra,” he wrote, “we consider only numbers, which represent quantities, without regarding the different kinds of quantity.”⁷ So, unless a line segment were somehow measured and thus represented by a number, Euler would not have considered it a legitimate unknown of an algebraic equation. Given, however, the close relationship between geometry and what was to evolve into algebra, we would be remiss here not to include line segments as possible unknowns in an equation, regardless of how they may be described, or line segments and areas as “knowns,” even if they are not measured. By the time our story has progressed into the nineteenth century, moreover, we shall see that the broadening of the mathematical horizon will make it necessary also to consider vectors, matrices, and other types of mathematical objects as unknowns in an equation.

Besides being vague, Euler’s definition, taken literally, is also quite broad. It encompasses what we generally think of as “arithmetic,” since the sum of 18 and 43 can be thought of as an “unknown” that can be expressed by the modern equation x = 18 + 43. To separate arithmetic from algebra, then, our historical analysis will generally be restricted to efforts to find unknowns that are linked to knowns in a more complicated way than just via an operation. This still leaves room for debate, however, as to what actually constitutes an “algebraic” problem. In particular, some of the earliest questions in which unknowns are sought involve what we term proportion problems, that is, problems solved through a version of the “rule of three,” namely, if

, then

. These appear in texts from ancient Egypt but also from Mesopotamia, India, China, Islam, and early modern Europe. Such problems are even found, in geometric guise, in classical Greek mathematics. However, al-Khwārizmīand his successors generally did not consider proportion problems in discussing their own science of al-jabr and al-muqābala. Rather, they preferred to treat them as part of “arithmetic,” that is, as a very basic part of the foundation of mathematical learning. In addition, such problems generally arose from real-world situations, and their solutions thus answered real-world questions. It would seem that in ancient times, even the solution of what we would call a linear equation in one variable was part of proportion theory, since such equations were frequently solved using “false position,” a method clearly based on proportions. Originally, then, such equations fell outside the concern of algebra, even though they are very much part of algebra now.

Given these historical vagaries, it is perhaps easiest to trace the development of algebra through the search for solutions to what we call quadratic equations. In the “West”—which, for us, will include the modern-day Middle East as far as India in light of what we currently know about the transmission of mathematical thought—a four-stage process can be identified in the history of this part of algebra. The first, geometric stage goes back some four millennia to Mesopotamia, where the earliest examples of quadratic equations are geometric in the sense that they ask for the unknown length of a side of a rectangle, for example, given certain relations involving the sides and the area. In general, problems were solved through manipulations of squares and rectangles and in purely geometric terms. Still, Mesopotamian mathematicians were flexible enough to treat quadratic problems not originally set in a geometric context by translating them into their geometric terminology. Mesopotamian methods for solving quadratic problems were also reflected in Greek geometric algebra, whether or not the Greeks were aware of the original context, as we...