The Fascinating World of Graph Theory

Arthur Benjamin, Gary Chartrand, Ping Zhang

• Publisher: Princeton University Press
• Year: 2015
• Print ISBN: 9780691175638, 9780691163819
• eBook ISBN: 9781400852000
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

The history, formulas, and most famous puzzles of graph theory

Graph theory goes back several centuries and revolves around the study of graphs—mathematical structures showing relations between objects. With applications in biology, computer science, transportation science, and other areas, graph theory encompasses some of the most beautiful formulas in mathematics—and some of its most famous problems. The Fascinating World of Graph Theory explores the questions and puzzles that have been studied, and often solved, through graph theory. This book looks at graph theory's development and the vibrant individuals responsible for the field's growth. Introducing fundamental concepts, the authors explore a diverse plethora of classic problems such as the Lights Out Puzzle, and each chapter contains math exercises for readers to savor. An eye-opening journey into the world of graphs, The Fascinating World of Graph Theory offers exciting problem-solving possibilities for mathematics and beyond.

1

Introducing Graphs

The mathematical structure known as a graph has the valuable feature of helping us to visualize, to analyze, to generalize a situation or problem we may encounter and, in many cases, assisting us to understand it better and possibly find a solution. Let’s begin by seeing how this might happen and what these structures look like.

FIRST, … FOUR PROBLEMS

We begin with four problems that have a distinct mathematical flavor. Yet any attempt to solve these problems doesn’t appear to use any mathematics you may have previously encountered. However, all of the problems can be analyzed and eventually solved with the aid of a relatively new sort of mathematical object and that object is a graph. The graph we’re referring to is not the kind of graph you’ve seen before. For example, Figure 1.1 shows the graph of the function y = sin x. That is not the kind of graph we’re referring to.

The Problem of the Five Princes

Once upon a time, there was a kingdom ruled by a king who had five sons. It was his wish that upon his death, this kingdom should be divided into five regions, one region for each son, such that each region would have a common boundary with each of the other four regions. Can this be done?

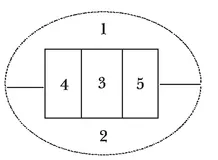
Figure 1.2 illustrates an unsuccessful attempt to satisfy the king’s wishes. Every two of the five regions, numbered 1, 2, 3, 4, 5, share some common boundary, except regions 4 and 5.

Figure 1.1. Not the sort of graph we’re talking about.

Figure 1.2. Attempting to satisfy the king’s wishes.

If the kingdom can be divided into five regions in the manner desired by the king, then something else would have to be true. Place a point in each region and join two points by a line or curve if the regions containing these points have a common boundary. If A and B are two adjacent regions in the kingdom and C and D are two other adjacent regions, then it’s always possible to connect each pair of points by a line in such a way that these two lines don’t cross.

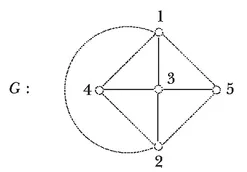
What we have just encountered is a graph (our type of graph) for the first time. A graph G is a collection of points (called vertices) and lines (called edges) where two vertices are joined by an edge if they are related in some way. In particular, the division of the kingdom into the five regions shown in Figure 1.2 gives rise to the graph G shown in Figure 1.3.

In order to have a solution to the king’s wishes, the resulting graph must have five vertices, every two joined by an edge. Such a graph is called a complete graph of order 5 and expressed as K₅. Furthermore, it must be possible to draw K₅ without any of its edges crossing. Since there is no edge joining vertices 4 and 5 in Figure 1.3, the division of the kingdom into regions shown in Figure 1.2 does not represent a solution. In Chapter 10 we will visit the Problem of the Five Princes again when we will be able to give a complete solution to this problem.

Figure 1.3. The graph representing the regions in Figure 1.2.

The Three Houses and Three Utilities Problem

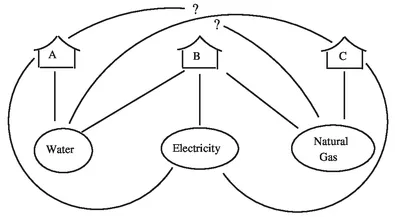
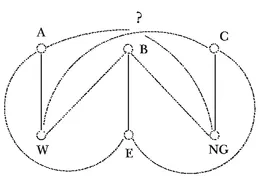
Three houses are under construction and each house must be provided with connections to each of three utilities, namely water, electricity and natural gas. Each utility provider needs a direct line from the utility terminal to each house without passing through another provider’s terminal or another house along the way. Furthermore, all three utility providers need to bury their lines at the same depth underground without any lines crossing. Can this be done?

Figure 1.4 shows a failed attempt to solve this problem, where the three houses are labeled A, B and C. Not only can this problem be looked at in terms of graphs, but in terms of graphs this problem is extremely similar to the Problem of the Five Princes. We can represent this situation by a graph with six vertices, three representing the three houses A, B and C and three representing the three utilities water (W), electricity (E) and natural gas (NG). Two vertices are joined by an edge when one vertex represents a house and the other represents a utility. This graph then has nine edges. This graph is denoted by K_3,3, indicating that there are two sets of three vertices each where each vertex in one set is joined to all vertices in the other set. To solve the Three Houses and Three Utilities Problem, we need to know whether K_3,3 can be drawn without any edges crossing. The attempted solution of the Three Houses and Three Utilities Problem in Figure 1.4 gives rise to the graph shown in Figure 1.5.

Figure 1.4. The Three Houses and Three Utilities Problem.

Figure 1.5. The graph representing the situation in Figure 1.4.

We will visit the Three Houses and Three Utilities Problem as well in Chapter 10 and explain how to solve the problem.

In our next problem a graph will be introduced whose vertices represent people. Here we assume every two people are friends or strangers.

The Three Friends or Three Strangers Problem

What is the smallest number of people that must be present at a gathering to be certain that among them three are mutual friends or three are mutual strangers?

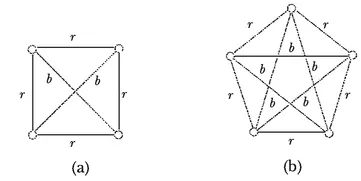
Figure 1.6. The answer to the Three Friends or Three Strangers Problem is neither four nor five.

Here too the situation can be represented by a graph, in fact by a complete graph. Suppose that four people are present at a gathering. Then we have a graph with four vertices, corresponding to the four people. We join every two vertices by an edge to indicate that these two people are friends or are strangers, resulting in the complete graph K₄ with four vertices and six edges. To indicate whether two people are friends or are strangers, we color the edge red (r) if the two people are friends and color the edge blue (b) if the two people are strangers. Thus three mutual friends would be represented by a red triangle in our graph and three mutual strangers would be represented by a blue triangle. The situation shown in Figure 1.6a shows that with four people it is possible to avoid having three mutual friends or three mutual strangers. Likewise, when we color the complete graph K₅ as in Figure 1.6b, we see that this situation can even be avoided with five people.

It turns out that the answer to the Three Friends or Three Strang...

Table of contents

• Cover Page
• Title Page
• Copyright Page
• Contents
• Preface
• Prologue
• 1 Introducing Graphs
• 2 Classifying Graphs
• 3 Analyzing Distance
• 4 Constructing Trees
• 5 Traversing Graphs
• 6 Encircling Graphs
• 7 Factoring Graphs
• 8 Decomposing Graphs
• 9 Orienting Graphs
• 10 Drawing Graphs
• 11 Coloring Graphs
• 12 Synchronizing Graphs
• Epilogue: Graph Theory: A Look Back—The Road Ahead
• Exercises
• Selected References
• Index of Names
• Index of Mathematical Terms