Fractional-Order Control Systems

Fundamentals and Numerical Implementations

Dingyü Xue

• Publisher: De Gruyter
• Year: 2017
• Print ISBN: 9783110499995
• eBook ISBN: 9783110497199
• Edition: 1
• Topic: Mathematics
• Subtopic: Differential Equations
• Index: Mathematics

This book explains the essentials of fractional calculus and demonstrates its application in control system modeling, analysis and design. It presents original research to find high-precision solutions to fractional-order differentiations and differential equations. Numerical algorithms and their implementations are proposed to analyze multivariable fractional-order control systems. Through high-quality MATLAB programs, it provides engineers and applied mathematicians with theoretical and numerical tools to design control systems.

Contents
Introduction to fractional calculus and fractional-order control
Mathematical prerequisites
Definitions and computation algorithms of fractional-order derivatives and Integrals
Solutions of linear fractional-order differential equations
Approximation of fractional-order operators
Modelling and analysis of multivariable fractional-order transfer function Matrices
State space modelling and analysis of linear fractional-order Systems
Numerical solutions of nonlinear fractional-order differential Equations
Design of fractional-order PID controllers
Frequency domain controller design for multivariable fractional-order Systems
Inverse Laplace transforms involving fractional and irrational Operations
FOTF Toolbox functions and models
Benchmark problems for the assessment of fractional-order differential equation algorithms

1Introduction to fractional calculus and fractional-order control

1.1Historical review of fractional calculus

In the earlier development of classical calculus, referred to in the book as integer-order calculus, the British scientist Sir Isaac Newton and the German mathematician Gottfried Wilhelm Leibniz used different symbols to denote different orders of derivatives to a function y(x): the notations Newton used were y'(x), y''(x), y'''(x), . . . , while Leibniz introduced the symbol dny(x)/dxn, where n is a positive integer.

In a letter from Guillaume François Antoine L’Hôpital, a French mathematician, to Leibniz in 1695, a specific question on the meaning of n = 1/2 was asked. In a letter dated 30 September 1695, Leibniz replied, “Thus it follows that d1/2x will be equal to $x\sqrt[2]{dx:x}$

, an apparent paradox, from which one day useful consequences will be drawn” [41]. The question and answer given above were considered as the beginning of fractional calculus. In 1819, it was shown by the French mathematician Sylvestre François Lacroix that the 1 /2th-order derivative of x is $2\sqrt{x/\pi }$

. It is obvious to see that the notations Newton used were not suitable to be extended to the field of fractional calculus, while the one by Leibniz was ready to be extended into the new field.

Three centuries passed, it was not until the last four or five decades, the research field concentrated on theoretical aspects. Very good historic reviews on the development of fractional calculus can be found in [41, 47], where in [41], Kenneth Miller and Bertram Ross presented a historic review of fractional calculus up to the last decade of the nineteenth century, while in [47], Keith Oldham and Jerome Spanier quoted Professor Bertram Ross’s year-by-year historic review of novel developments in fractional calculus up to the year 1975. These reviews were mainly focused on the development in pure mathematics.

From 1960s, the fractional calculus research was extended into engineering fields. The dissipation model based on fractional-order derivatives was proposed by Professors Michele Caputo and Francesco Mainardi in Italy [5]. Professor Shunji Manabe in Japan extended the theoretical work to the field of control systems and introduced the non-integer-order control systems [36]. Professor Igor Pudlubny in Slovakia proposed the structures and applications of fractional-order PID controllers [55]. The work of Professor Alain Oustaloup’s group in France on robust controller design and their applications in suspension control systems in automobile industry [48, 49] was considered as a milestone in real-world applications of fractional calculus.

From the years around 2000, several monographs dedicated to fractional calculus and its applications in a variety of fields appeared, among those, the well-organised ones are Professor Igor Podlubny’s book [54] on fractional-order differential equations and automatic control in 1999, Professor Rudolf Hilfer’s book [23] in physics in 2000, and Professor Richard Magin’s book [35] in bioengineering in 2002.

Recently, several books concentrating on numerical computation and theoretical aspects in fractional calculus were published, such as Kai Diethelm’s book [16] in 2010, Shantanu Das’s book [13] in 2011, Vladimir Uchaikin’s book [66] in 2013, and Changpin Li and Fanhai Zeng’s book [28] in 2015.

Many books on fractional-order control were published, for instance, Riccardo Caponetto, Giovanni Dongola, Luigi Fortuna and Ivo Petráš’s book [4] in 2010, Concepción Monje, YangQuan Chen, Blas Vinagre, Dingyü Xue and Vicente Feliu’s book [42] in 2010, Ivo Petráš’s book [52] in 2011, Ying Luo and YangQuan Chen’s book [33] in 2012, and Alain Oustaloup’s book [50] in 2014. The book [67] by Vladimir Uchaikin in 2013 delivered a very comprehensive coverage on the applications of fractional calculus in a variety of fields.

It should be noted that the terms “fractional” or “fractional-order” are misused ones; more suitable terms are “non-integer-order” or “arbitrary-order”, since apart from fractional (rational) numbers, the theory also includes irrational numbers, for instance, $d^{\sqrt{2}}y\left(t\right)/d{t}^{\sqrt{2}}$

, or even, n can be a complex number, while this is beyond the scope of the book. Since in the literature and in the related research communities, the term “fractional” is extensively used, in the book we use this term as well, while it also includes irrational-orders, and even the structures of the system are irrational.

We shall use the unified terms “fractional calculus”, “fractional-order systems” and “fractional-order derivatives” throughout the book.

As is well known in classical calculus, if x is the displacement, then dx/dt is the velocity, while d2x/dt2 is the acceleration. Unfortunately, there are almost no wi...

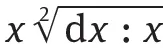
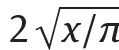
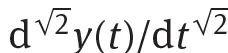
Table of contents

• Cover
• Title Page
• Copyright
• Foreword
• Preface
• Contents
• 1 Introduction to fractional calculus and fractional-order control
• 2 Mathematical prerequisites
• 3 Definitions and computation algorithms of fractional-order derivatives and integrals
• 4 Solutions of linear fractional-order differential equations
• 5 Approximation of fractional-order operators
• 6 Modelling and analysis of multivariable fractional-order transfer function matrices
• 7 State space modelling and analysis of linear fractional-order systems
• 8 Numerical solutions of nonlinear fractional-order differential equations
• 9 Design of fractional-order PID controllers
• 10 Frequency domain controller design for multivariable fractional-order systems
• A Inverse Laplace transforms involving fractional and irrational operations
• B FOTF Toolbox functions and models
• C Benchmark problems for the assessment of fractional-order differential equation algorithms
• Bibliography
• Index