Minkowski Space

The Spacetime of Special Relativity

Joachim Schröter, Christian Pfeifer

• Publisher: De Gruyter
• Year: 2017
• Print ISBN: 9783110484571
• eBook ISBN: 9783110484618
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Geometry

In Minkowski-Space the space-time of special relativity is discussed on the basis of fundamental results of space-time theory. This idea has the consequence that the Minkowski-space can be characterized by 5 axioms, which determine its geometrical and kinematical structure completely. In this sense Minkowski-Space is a prolegomenon for the formulation of other branches of special relativity, like mechanics, electrodynamics, thermodynamics etc. But these applications are not subjects of this book.

Contents

Basic properties of special relativity
Further properties of Lorentz matrices
Further properties of Lorentz transformations
Decomposition of Lorentz matrices and Lorentz transformations
Further structures on M s
Tangent vectors in M s
Orientation
Kinematics on M s
Some basic notions of relativistic theories

1Basic properties of special relativity

1.1Special relativity as a special case of general relativity

1.1.1

The following definition is the basis of the spacetime structure of special realativity:

Definition 1.1. Minkowski spacetime or short Minkowski space is a manifold 𝓜s = (Ms , 𝓐s , gs) for which the following holds:

(1)Ms is a set.

(2)𝓐s is a Ck -Atlas on Ms with k ≥ 3.

(3)There exists a global chart (Ms , φ) in 𝓐s , i.e.,

$\phi :M^S\to {ℝ}^4$

is bijective.

(4)gs is a (0, 2)-tensor field on Ms , called metric.

(5)In the coordinates x = φ(p), p ∈ Ms defined by the global chart (Ms , φ) the metric takes the form

${\text{g}}^{\text{S}}(p)=d{x}^1\otimes d{x}^1+d{x}^2\otimes d{x}^2+d{x}^3\otimes d{x}^3-d{x}^4\otimes d{x}^4.$

Properties (1) and (2) (with k ≥ 1) are the usual axioms of differentiable manifolds (Section 9.1). It follows that at every point p ∈ 𝓜s there exists a tangent vector space Tp𝓜s (Section 9.2) and its dual, the cotangent vector space $T_p^{*}{M}^S$

(Section 9.3), as well as all of their tensor products (Section 9.6) and the corresponding differentiable tensor fields (Section 9.7). Properties (1)–(5) specify that 𝓜s is a semi-Riemannian manifold (Section 9.7), by the fact that the metric gs(p) is an indefinite inner product in the tangent vector spaces Tp𝓜s (Section 9.4). The objects dxκ , κ = 1, . . . , 4, used to formulate the metric in equation (1.2) are basis vectors in $...$

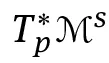
Table of contents

• Cover
• Title Page
• Copyright
• Contents
• Introduction
• 1 Basic properties of special relativity
• 2 Further properties of Lorentz matrices
• 3 Further properties of Lorentz transformations
• 4 Decomposition of Lorentz matrices and Lorentz transformations
• 5 Further structures on Ms
• 6 Tangent vectors in 𝓜s
• 7 Orientation
• 8 Kinematics on Ms
• 9 Some basic notions of relativistic theories
• Epilogue
• Bibliography
• Index