Recent Developments In Computational Finance: Foundations, Algorithms And Applications

Foundations, Algorithms and Applications

Thomas Gerstner, Peter Kloeden

• Publisher: WSPC
• Year: 2012
• Print ISBN: 9789814436427
• eBook ISBN: 9789814436441
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

Computational finance is an interdisciplinary field which joins financial mathematics, stochastics, numerics and scientific computing. Its task is to estimate as accurately and efficiently as possible the risks that financial instruments generate. This volume consists of a series of cutting-edge surveys of recent developments in the field written by leading international experts. These make the subject accessible to a wide readership in academia and financial businesses.

The book consists of 13 chapters divided into 3 parts: foundations, algorithms and applications. Besides surveys of existing results, the book contains many new previously unpublished results.

Contents:

• Foundations:
  • Multilevel Monte Carlo Methods for Applications in Finance (Mike Giles and Lukasz Szpruch)
  • Convergence of Numerical Methods for SDEs in Finance (Peter Kloeden and Andreas Neuenkirch)
  • Inverse Problems in Finance (J Baumeister)
  • Asymptotic and Non Asymptotic Approximations for Option Valuation (R Bompis and E Gobet)
• Algorithms:
  • Discretization of Backward Stochastic Volterra Integral Equations (Christian Bender and Stanislav Pokalyuk)
  • Semi-Lagrangian Schemes for Parabolic Equations (Kristian Debrabant and Espen Robstad Jakobsen)
  • Derivative-Free Weak Approximation Methods for Stochastic Differential Equations (Kristian Debrabant and Andreas Röβler)
  • Wavelet Solution of Degenerate Kolmogoroff Forward Equations (Oleg Reichmann and Christoph Schwab)
  • Randomized Multilevel Quasi-Monte Carlo Path Simulation (Thomas Gerstner and Marco Noll)
• Applications:
  • Drift-Free Simulation Methods for Pricing Cross-Market Derivatives with LMM (J L Fernández, M R Nogueiras, M Pou and C Vázquez)
  • Application of Simplest Random Walk Algorithms for Pricing Barrier Options (M Krivko and M V Tretyakov)
  • Coupling Local Currency Libor Models to FX Libor Models (John Schoenmakers)
  • Dimension-Wise Decompositions and Their Efficient Parallelization (Philipp Schröder, Peter Mlynczak and Gabriel Wittum)

Readership: Graduate students and researchers in finance, engineering and operations research.

PART 1

Foundations

Chapter 1

Multilevel Monte Carlo methods for applications in finance

Mike Giles and Lukasz Szpruch

Oxford-Man Institute of Quantitative Finance
and Mathematical Institute, University of Oxford

Abstract Since Giles introduced the multilevel Monte Carlo path simulation method [18], there has been rapid development of the technique for a variety of applications in computational finance. This paper surveys the progress so far, highlights the key features in achieving a high rate of multilevel variance convergence, and suggests directions for future research.

1. Introduction

In 2001, Heinrich [28], developed a multilevel Monte Carlo method for parametric integration, in which one is interested in estimating the value of

[f(x,

)] where x is a finite-dimensional random variable and

is a parameter. In the simplest case in which

is a real variable in the range [0,1], having estimated the value of

[f(x,0)] and

[f(x,1)], one can use

as a control variate when estimating the value of

, since the variance of

will usually be less than the variance of

. This approach can then be applied recursively for other intermediate values of

, yielding large savings if f(x,

) is sufficiently smooth with respect to

.

Giles’ multilevel Monte Carlo path simulation [18] is both similar and different. There is no parametric integration, and the random variable is infinite-dimensional, corresponding to a Brownian path in the original paper. However, the control variate viewpoint is very similar. A coarse path simulations is used as a control variate for a more refined fine path simulation, but since the exact expectation for the coarse path is not known, this is in turn estimated recursively using even coarser path simulation as control variates. The coarsest path in the multilevel hierarchy may have only one timestep for the entire interval of interest.

A similar two-level strategy was developed slightly earlier by Kebaier [31], and a similar multi-level approach was under development at the same time by Speight [42;43].

In this review article, we start by introducing the central ideas in multilevel Monte Carlo simulation, and the key theorem from [18] which gives the greatly improved computational cost if a number of conditions are satisfied. The challenge then is to construct numerical methods which satisfy these conditions, and we consider this for a range of computational finance applications.

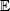
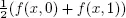
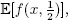
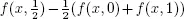
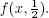
2. Multilevel Monte Carlo

2.1. Monte Carlo

Monte Carlo simulation has become an essential tool in the pricing of derivatives security and in risk management. In the abstract setting, our goal is to numerically approximate the expected value

[Y ], where Y = P(X) is a functional of a random variable X. In most financial applications we are not able to sample X directly and hence, in order to perform Monte Carlo simulations we a...

Table of contents

• Cover Page
• Halftitle
• Series
• Title
• Copyright
• Contents
• Preface
• Foundations
• Algorithms
• Applications