Localisation 2011 - Proceedings Of The Satellite Conference Of Lt 26

Stefan Kettemann

• Publisher: WSPC
• Year: 2012
• Print ISBN: 9789814436854
• eBook ISBN: 9789814436878
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

The proceedings of Localisation 2011, a satellite conference of the 26th International Conference on Low Temperature Physics (LT26), comprise both invited and contributed papers that discuss the latest progress on localisation phenomena. The main topics include quantum transport in disordered systems (Anderson localisation, effects of interactions on localisation, Anderson–Mott transition, mesoscopics), the superconductor–insulator transition, quantum Hall effects (fractional and integer), topological insulators, graphene, dynamical localisation, heavy fermions (Kondo effect, Kondo lattice, effects of disorder), and many body localisation (spin-glass, Coulomb glass). The volume is also dedicated to Professor Bernard Coqblin, former CNRS Directeur de Recherche and a Honorary Chairman of the AMS-APCTP Conference Localisation 2011, whose contribution to condensed matter theory will always be remembered.

Contents:

• Wave Propagation and Localization via Quasi-Normal Modes and Transmission Eigenchannels (J Wang, Z Shi, M Davy and A Z Genack)
• Quantized Intrinsically Localized Modes: Localization Through Interaction (P S Riseborough)
• Aspects of Localization Across the 2D Superconductor–Insulator Transition (N Trivedi, Y L Loh, K Bouadim and M Randeria)
• The Spin Glass-Kondo Competition in Disordered Cerium Systems (S G Magalhaes, F Zimmer and B Coqblin)
• Transport via Classical Percolation at Quantum Hall Plateau Transitions (M Flöser, S Florens and T Champel)
• Finite Size Scaling of the Chalker–Coddington Model (K Slevin and T Ohtsuki)
• Bulk and Edge Quasihole Tunneling Amplitudes in the Laughlin State (Z-X Hu, K H Lee and X Wan)
• “Rare” Fluctuation Effects in the Anderson Model of Localization (R N Bhatt and S Johri)
• Effect of Electron–Electron Interaction Near the Metal–Insulator Transition in Doped Semiconductors Studied within the Local Density Approximation (Y Harashima and K Slevin)
• Can Diffusion Model Localization in Open Media? (C-S Tian, S-K Cheung and Z-Q Zhang)
• Local Pseudogaps and Free Magnetic Moments at the Anderson Metal–Insulator Transition: Numerical Simulation Using Power-Law Band Random Matrices (I Varga, S Kettemann and E R Mucciolo)
• Finite Size Scaling of the Typical Density of States of Disordered Systems within the Kernel Polynomial Method (D Jung, G Czycholl and S Kettemann)
• Critical Exponent for the Quantum Spin Hall Transition in ℤ 2 Network Model (K Kobayashi, T Ohtsuki and K Slevin)
• Disorder Induced BCS–BEC Crossover (A Khan)
• A Comparison of Harmonic Confinement and Disorder in inducing Localization Effects in a Superconductor (P Dey, A Khan, S Basu and B Tanatar)
• Quasi Two-Dimensional Nucleon Superfluidity Under Localization with Pion Condensation (T Takatsuka)
• Enhancement of Graphene Binding Energy by Ti 1ML Intercalation between Graphene and Metal Surfaces (T Kaneko and H Imamura)
• Generalization of Chiral Symmetry for Tilted Dirac Cones (T Kawarabayashi, Y Hatsugai, T Morimoto and H Aoki)
• Electronic States and Local Density of States Near Graphene Corner Edge (Y Shimomura, Y Takane and K Wakabayashi)
• Perfectly Conducting Channel and Its Robustness in Disordered Carbon Nanostructures (Y Ashitani, K-I Imura and Y Takane)
• Direction Dependence of Spin Relaxation in Confined Two-Dimensional Systems (P Wenk and S Kettemann)
• Analysis of Quantum Corrections to Conductivity and Thermopower in Graphene — Numerical and Analytical Approaches (A P Hinz, S Kettemann and E R Mucciolo)
• Indirect Exchange Interactions in Graphene (H Lee, E R Mucciolo, G Bouzerar and S Kettemann)
• Critical Exponents for Antiferromagnetic Spin Chains Obtained from Bosonisation (M Kossow, P Schupp and S Kettemann)

Readership: Academics and scientists interested in condensed matter physics.

EFFECT OF ELECTRON-ELECTRON INTERACTION NEAR THE METAL-INSULATOR TRANSITION IN DOPED SEMICONDUCTORS STUDIED WITHIN THE LOCAL DENSITY APPROXIMATION

YOSUKE HARASHIMA and KEITH SLEVIN*

Department of Physics, Graduate School of Science, Osaka University,
1-1 Machikaneyama, Toyonaka, Osaka 560-0043, Japan
* [email protected]

Revised 4 April 2012

We report a numerical analysis of Anderson localization in a model of a doped semiconductor. The model incorporates the disorder arising from the random spatial distribution of the donor impurities and takes account of the electron-electron interactions between the carriers using density functional theory in the local density approximation. Preliminary results suggest that the model exhibits a metal-insulator transition.

Keywords: disordered system; metal-insulator transition; density functional theory, Anderson localization.

PACS numbers: 71.23.An, 71.30.+h, 71.15.Mb

1. Introduction

In semiconductors a zero temperature metal-insulator transition is observed as a function of doping concentration. For samples with concentrations below a critical concentration, the conductivity extrapolated to zero temperature is found to be zero. For samples with concentrations exceeding this critical concentration, the zero temperature limit of the conductivity is finite.¹ One well studied example is phosphor doped silicon (Si:P) (see Ref. 2 for a recent review). The relative importance of the roles that electron-electron interactions and disorder play in this transition is still not clear. The Coulomb interaction between the electrons leads us to expect that the impurity band is split into upper and lower Hubbard bands and that the transition is associated with a closing of the Hubbard gap. However, this ignores the effect of the disorder that arises from the random spatial distribution of the donor impurities and the possibility of Anderson localization.³ This paper is a preliminary report of numerical simulations designed to address this issue.

2. Model

As a simple model of a doped semiconductor we consider an effective medium with electron effective mass

and dielectric constant ε_r equal to those of the host semiconductor crystal. In this effective medium N donor impurities are randomly distributed in space. Since we have mind phosphor in silicon, we assume that each donor supplies one electron and as a result has a net charge of +e. This is the only property of the donor which enters our model. There are an equal number of electrons so that the total charge is zero. The electrons interact with the donors through the Coulomb interaction. The random spatial distribution of the donors thus produces a random potential in which the electrons move. At the same time the electrons interact with each other via the Coulomb interaction. The Hamiltonian of this system is

Here, Hartree atomic units are used. The positions of the donor impurities are denoted by

. The first term is the kinetic energy of the electrons, the second term describes the interaction of the electrons with the donor impurities, and the third term describes the interaction between the electrons. A fourth term describing the mutual Coulomb interaction between the donor impurities should also be included if the correct total energy of the system is required. However, since the positions of the donor impurities, while random, are fixed, this contribution to the energy does not play any role in the following discussion and is, therefore, omitted.

To deal with the electron-electron interaction we use density functional theory⁴ and solve the Kohn-Sham equations⁵ that describe an auxiliary one-electron problem that has the same ground state density as the interacting problem of Eq. (1). The Kohn-Sham equations are

where

The number density of the electrons is

Periodic boundary conditions are imposed. In this model the dependence on the medium enters only through the effective mass and dielectric constant. Having in mind silicon as the host semiconductor we set

The exchange-correlation potential appearing in the Kohn-Sham equations is given by the functional derivative of the exchange-correlation energy with respect to the number density of electrons

While in principle the Kohn-Sham equations are exact, in practice the exact form of the exchange-correlation potential is not known and an approximation is required. In this work, we use the local density approximation (LDA) in which the functional is approximated as

In this preliminary work, we assume complete spin polarization.^a We use the form of Є_XC given in Eq. (2) of Ref. 6 (with spin polarization ζ = 1) though with the parameter values given in Ref. 7 rather than Ref. 6.

In the literature expressions for the exchange-correlation potential are given for electrons in free space whereas we are considering an effective medium. To map the expressions in the literature to the formulae we require here, we re-scale lengths and energies according to the formulae

After this re-scaling we have

where

and

is the exchange-correlation potential found in the literature.

In Hartree ...

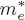
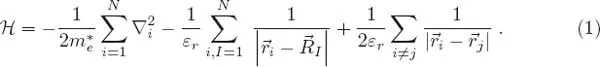
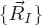
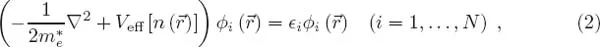
Table of contents

• Cover Page
• Title Page
• Copyright Page
• Preface
• Contents
• Invited Talks
• Contributed Talks