Path Integrals For Stochastic Processes: An Introduction

An Introduction

Horacio S Wio

• Publisher: WSPC
• Year: 2013
• Print ISBN: 9789814447997
• eBook ISBN: 9789814449052
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

This book provides an introductory albeit solid presentation of path integration techniques as applied to the field of stochastic processes. The subject began with the work of Wiener during the 1920's, corresponding to a sum over random trajectories, anticipating by two decades Feynman's famous work on the path integral representation of quantum mechanics. However, the true trigger for the application of these techniques within nonequilibrium statistical mechanics and stochastic processes was the work of Onsager and Machlup in the early 1950's. The last quarter of the 20th century has witnessed a growing interest in this technique and its application in several branches of research, even outside physics (for instance, in economy).

The aim of this book is to offer a brief but complete presentation of the path integral approach to stochastic processes. It could be used as an advanced textbook for graduate students and even ambitious undergraduates in physics. It describes how to apply these techniques for both Markov and non-Markov processes. The path expansion (or semiclassical approximation) is discussed and adapted to the stochastic context. Also, some examples of nonlinear transformations and some applications are discussed, as well as examples of rather unusual applications. An extensive bibliography is included. The book is detailed enough to capture the interest of the curious reader, and complete enough to provide a solid background to explore the research literature and start exploiting the learned material in real situations.

Contents:

• Stochastic Processes: A Short Tour
• The Path Integral for a Markov Stochastic Process
• Generalized Path Expansion Scheme I
• Space-Time Transformation I
• Generalized Path Expansion Scheme II
• Space-Time Transformation II
• Non-Markov Processes: Colored Noise Case
• Non-Markov Processes: Non-Gaussian Case
• Non-Markov Processes: Nonlinear Cases
• Fractional Diffusion Process
• Feynman–Kac Formula, the Influence Functional
• Other Diffusion-Like Problems
• What was Left Out

Readership: Advanced undergraduate and graduate students, researchers interested in stochastic analysis and statistical physics.

Chapter 1

Stochastic Processes: A Short Tour

1.1 Stochastic Process

We start this section by writing the evolution equation for a one dimensional dynamical system (Haken (1978); Wio (1994); Nicolis (1995); Wio (1997))

where x corresponds to the state variable while ζ is a control parameter. Such a parameter could be, for instance, the temperature, an external field, a reactant's controlled flux, etc, indicating the form in which the system is coupled to its surroundings. Experience tells us that it is usually impossible to keep the value of such parameters fixed, and consequently that fluctuations become relevant. Hence, the original deterministic equation will acquire a random or stochastic character.

Among the many reasons justifying the growing interest in the study of fluctuations we can point out that they present a serious impediment to accurate measurements in very sensitive experiments, demanding some very specific techniques in order to reduce their effects, and that the fluctuations might be used as an additional source of information about the system. But maybe the most important aspect is that fluctuations can produce macroscopic effects contributing to the appearance of some form of noise-induced order like space-temporal patterns or dissipative structures (Horsthemke and Lefever (1984); Nicolis (1995); Wio (1994); Walgraef (1997); Wio (1997); Gammaitoni et al. (1998); Reimann (2002); Wio, et al. (2002); Lindner et al. (2004); Sagues et al. (2007); Wio and Deza (2007); Wio, Deza and L

pez (2012)).

The general character of the evolution equations of dynamical systems makes it clear why stochastic methods have become so important in different branches of physics, chemistry, biology, technology, population dynamics, economy, and sociology. In spite of the large number of different problems that arise in all these fields, there are some common principles and methods that are included in a global framework: the theory of stochastic processes. Here we will only briefly review the few aspects relevant for our present needs. For deeper study we refer to van Kampen (2004); Risken (1983); Horsthemke and Lefever (1984); Gardiner (2009); Wio (1994); Lindenberg and Wio (2003); Wio, Deza and L

pez (2012).

In order to include the presence of fluctuations into our description, we write ζ = ζ₀ + ξ(t), where ζ₀ is a constant value and ξ(t) is the random or fluctuating contribution to the parameter ζ. The simplest (or lowest order) form that equation (1.1) can adopt is

The original deterministic differential equation has been transformed into a stochastic differential equation (SDE), where ξ(t) is called a noise term or stochastic process.

Any stochastic process x(t) is completely specified if we know the complete hierarchy of probability densities. We write

for the probability that x(t₁) is within the interval (x₁,x₁ + dx₁),x(t₂) in (x₂, x₂ + dx₂), and so on. These P_n may be defined for n = 1,2,…., and only for different times. This hierarchy fulfills some properties

i) P_n ≥ 0

ii) P_n is invariant under permutations of pairs (x_i,t_i) and (x_j,t_j)

iii) ∫ P_n dx_n = P_n-1, and , ∫ P₁ dx₁ = 1.

Another important quantity is the conditional probability density P_n/m that corresponds to the probability of having the value x₁ at time t₁,x₂ at t₂,…,x_n at t_n; given that we have x(t_n+1) = x_n+1,x(t_n+2) = x_n+2,x(t_n+3) = x_n+3,… ,x(t_n+m) = x_n+m.Its definition is

Among the many possible classes of stochastic processes, there is one that plays a central role: Markov Processes (van Kampen (2004); Risken (1983); Gardiner (2009); Wio (1994); Lindenberg and Wio (2003)). For a stochastic process x(t),

is the conditiona...

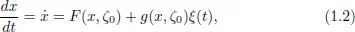
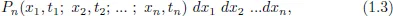
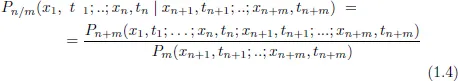
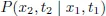
Table of contents

• Cover
• Halftitle
• Title Page
• Copyright Page
• Contents
• Preface
• 1. Stochastic Processes: A Short Tour
• 2. The Path Integral for a Markov Stochastic Process
• 3. Generalized Path Expansion Scheme I
• 4. Space-Time Transformation I
• 5. Generalized Path Expansion Scheme II
• 6. Space-Time Transformation II
• 7. Non-Markov Processes: Colored Noise Case
• 8. Non-Markov Processes: Non-Gaussian Case
• 9. Non-Markov Processes: Nonlinear Cases
• 10. Fractional Diffusion Process
• 11. Feynman-Kac Formula, the Influence Functional
• 12. Other Diffusion-Like Problems
• 13. What was Left Out
• Appendix A. Space-Time Transformation: Definitions and Solutions
• Appendix B. Basics Definitions in Fractional Calculus
• Bibliography
• Index