The International Mathematical Olympiad (IMO) is a competition for high school students. China has taken part in the IMO 21 times since 1985 and has won the top ranking for countries 14 times, with a multitude of golds for individual students. The six students China has sent every year were selected from 20 to 30 students among approximately 130 students who took part in the annual China Mathematical Competition during the winter months. This volume of comprises a collection of original problems with solutions that China used to train their Olympiad team in the years from 2009 to 2010. Mathematical Olympiad problems with solutions for the years 2002–2008 appear in an earlier volume, Mathematical Olympiad in China.
Contents:
2008–2009 China Mathematical Competition
2008–2009 China Mathematical Competition (Complementary Test)
2009–2010 China Mathematical Olympiad
2009–2010 China National Team Selection Test
2008–2009 China Girls' Mathematical Olympiad
2008–2009 China Western Mathematical Olympiad
2009–2010 China Southeastern Mathematical Olympiad
2009–2010 International Mathematical Olympiad
Readership: Mathematics students, school teachers, college lecturers, university professors; mathematics enthusiasts.
Frequently asked questions
Yes, you can cancel anytime from the Subscription tab in your account settings on the Perlego website. Your subscription will stay active until the end of your current billing period. Learn how to cancel your subscription.
At the moment all of our mobile-responsive ePub books are available to download via the app. Most of our PDFs are also available to download and we're working on making the final remaining ones downloadable now. Learn more here.
Perlego offers two plans: Essential and Complete
Essential is ideal for learners and professionals who enjoy exploring a wide range of subjects. Access the Essential Library with 800,000+ trusted titles and best-sellers across business, personal growth, and the humanities. Includes unlimited reading time and Standard Read Aloud voice.
Complete: Perfect for advanced learners and researchers needing full, unrestricted access. Unlock 1.4M+ books across hundreds of subjects, including academic and specialized titles. The Complete Plan also includes advanced features like Premium Read Aloud and Research Assistant.
Both plans are available with monthly, semester, or annual billing cycles.
We are an online textbook subscription service, where you can get access to an entire online library for less than the price of a single book per month. With over 1 million books across 1000+ topics, we’ve got you covered! Learn more here.
Look out for the read-aloud symbol on your next book to see if you can listen to it. The read-aloud tool reads text aloud for you, highlighting the text as it is being read. You can pause it, speed it up and slow it down. Learn more here.
Yes! You can use the Perlego app on both iOS or Android devices to read anytime, anywhere — even offline. Perfect for commutes or when you’re on the go. Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Yes, you can access Mathematical Olympiad In China (2009-2010): Problems And Solutions by Bin Xiong, Peng Yee Lee in PDF and/or ePUB format, as well as other popular books in Mathematics & History & Philosophy of Mathematics. We have over one million books available in our catalogue for you to explore.
Let D be a point on side BC of triangle ABC such that
CAD =
CBA. A circle with center O passes through B, D, and meets segments AB, AD at E, F, respectively. Lines BF and DE meet at point G. M is the midpoint of AG. Prove that CM
AO. (Posed by Xiong Bin)
Proof As shown in Fig. 1, extend EF and meet BC at point P, and join and extend GP, which meets AD at K and the extension of AC at L.
Fig. 1
As shown in Fig. 2, let Q be a point on AP such that
PQF =
AEF =
ADB.
It is easy to see that A, E, F, Q and F, D, P, Q are concyclic respectively. Denote by r the radius of
O. By the power of a point theorem,
Fig. 2
Similarly,
By
,
, we have AP2 − AG2 = PO2 − GO2, which implies that PG
AO. As shown in Fig. 3, applying Menelaus’ theorem for ΔPFD and line AEB, we have
Applying Ceva's theorem for ΔPFD and point G, we have
yields
Fig. 3
Equation
illustrates that A, K are harmonic points with respect to F, D, i.e. AF × KD = AD × FK.
It follows that
...
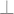
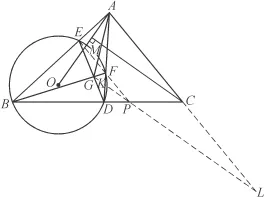
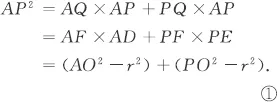
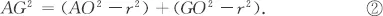
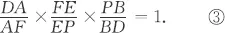
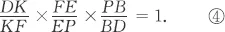
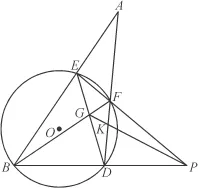
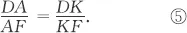
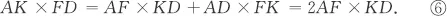
Table of contents
Cover
Title Pagina
Copyright
Editors
Preface
Introduction
China Mathematical Competition
China Mathematical Competition (Complementary Test)
