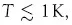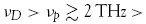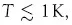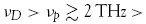Glassy Disordered Systems: Glass Formation And Universal Anomalous Low-energy Properties (Soft Modes)

Glass Formation and Universal Anomalous Low-Energy Properties

Michael I Klinger

• Publisher: WSPC
• Year: 2013
• ISBN:
  9789814407496
• Topic: Tecnología e ingeniería
• Subtopic: Ciencias de los materiales

The present book describes the fundamental features of glassy disordered systems at high temperatures (close to the liquid-to-glass transition) and for the first time in a book, the universal anomalous properties of glasses at low energies (i.e. temperatures/frequencies lower than the Debye values) are depicted. Several important theoretical models for both the glass formation and the universal anomalous properties of glasses are described and analyzed. The origin and main features of soft atomic-motion modes and their excitations, as well as their role in the anomalous properties, are considered in detail. It is shown particularly that the soft-mode model gives rise to a consistent description of the anomalous properties. Additional manifestations of the soft modes in glassy phenomena are described. Other models of the anomalous glassy properties can be considered as limit cases of the soft-mode model for either very low or moderately low temperatures/frequencies.

Contents:

• Fundamental Properties of Glasses:
  • General Description of Glasses and Glass Transition
  • Models of Glassy (Topologically Disordered) Structures
  • Some Theoretical Models of Glass Transition
  • Kohlrausch–William–Watt (KWW) Relaxation
• Anomalous Low-Energy Dynamics of Glasses:
  • Origin of Anomalous Low-Energy Properties of Glasses
  • Experimental Background for Anomalous Low-Energy Atomic Dynamics
  • Soft-Mode Model of Low-Energy Atomic Dynamics
  • Soft-Mode Excitations of Very Low and “Intermediate” Energies
  • Tunneling States as Very Low Energy Limit Case
  • Soft-Mode Excitations of Moderately-Low Energies (Boson Peak)
  • On Universal and Non-Universal Dynamic Properties of Glasses
  • Other Models for Glasses with High Frequency Sound
  • Recent Models for Glasses with No High-Frequency Sound
  • Anomalous Electron Properties of Semiconducting Glasses
  • Soft-Mode Model of Localized Electron States in the Glasses
  • Additional Manifestations of Soft Modes in Glasses
  • Summary, Conclusions and Problems

Readership: Graduate students in the field of amorphous solids, professional theoretical physicists in glasses, professional experimentalists in glasses.

PART II

ANOMALOUS LOW-ENERGY DYNAMICS OF GLASSES

5

ORIGIN OF ANOMALOUS LOW-ENERGY PROPERTIES OF GLASSES

The primary goal of the second part of the present book is to discuss a consistent description of the theoretical soft-mode model, the nature of atomic-motion soft modes and the role of the modes in anomalous properties of glasses, far below the liquid–glass transition. As seen in what follows, the properties (at least of a series of glasses) can be consistently described within the framework of this model, and some predictions can be made for experimental tests. The properties include the experimentally observed and studied dynamic and thermal properties of glasses at low frequencies υ << υ_D and/or low temperatures T << T_D = _hυ_D/k_B ≡ hυ_D, where υ_D and T_D are the effective Debye frequency and temperature respectively (as well as in part A, in what follows the Boltzmann constant k_B = 1). These properties are often referred to as anomalous properties in the sense that they are not characteristic of the crystalline counterparts. The most widely known anomalous properties of glasses appear to be the T - and T² temperature dependence of specific heat and thermal conductivity respectively at very low temperatures,

discovered by Zeller and Pohl in 1971 [104], and the so-called “boson peak”, a broad asymmetric peak in photon or neutron inelastic scattering intensity at a moderately low frequency shift (below referred to as frequency) υ = υ_BP ≈ 1 THz, which is not characteristic of crystals. Since that time, the anomalous properties of glasses have been investigated in numerous works (e.g., [105, 106, 107, 109, 110, 111, 112]) and are referred to as universal properties in the sense that they are also weakly sensitive to differences in chemical composition and local atomic structures of the materials. Let us emphasize that the above does not contradict the experimental fact that in a few crystals, e.g., in the cristobalite polymorph of S_iO₂, a peak is also observed in the reduced inelastic neutron scattering intensity, i.e. in the reduced vibrational density of states [7], at a noticeably higher υ = υ_p, e.g., at

υ_BP, which can be sometimes related to the lowest van Hove singularity of the crystal [113]. This and other differences between low-energy properties of glasses and those of respective crystals show that the anomalous properties under discussion in what follows characterize glassy, amorphous systems, rather than crystals. In other words, the amorphous, glassy state of the system in general appears to be a necessary condition for the boson peak existence.

Taking into account the above-mentioned primary goal and, on the other hand, the very large number of investigations of the anomalous dynamic and thermal properties of glasses, the present review also describes, for comparison, other (not explicitly related to the soft-mode model) recent theoretical models of the glassy properties. The soft-mode model appears to be the only model that is able to describe, qualitatively and in scale at least, the glassy properties at both very low and moderately low frequencies and temperatures. In the section below, we concentrate on the soft-mode model and anomalous, universal properties of nonmetallic (insulating and semiconducting) glasses, for which the role of electronic excitations and their interaction with other excitations are not so important (for metallic glasses the properties are considered in detail in a number of reviews, in particular, in [8, 9]).

In accordance with a general concept of solid state theory [115] that explains the properties of a material as due to the existence of appropriate elementary excitations and their interactions, the deviations of dynamic and thermal properties of glasses from Debye ones of crystalline materials at low υ << υ_D and T << T_D can be attributed to the occurrence of excess excitations of low energy ε << hυ...

Table of contents

• Cover Page
• Title Page
• Copyright Page
• Contents
• Preface
• I.   Fundamental Properties of Glasses
• II.   Anomalous Low-Energy Dynamics of Glasses
• Appendix A. Convolution of Soft-Mode Vibrational DOS and Transformation Kernel in the DOS of BP and HFS Excitations
• References
• Index