Non-axiomatic Logic: A Model Of Intelligent Reasoning

A Model of Intelligent Reasoning

Pei Wang

• Publisher: WSPC
• Year: 2013
• Print ISBN: 9789814440271
• eBook ISBN: 9789814440295
• Topic: Computer Science
• Subtopic: Artificial Intelligence (AI) & Semantics
• Index: Computer Science

This book provides a systematic and comprehensive description of Non-Axiomatic Logic, which is the result of the author's research for about three decades.

Non-Axiomatic Logic is designed to provide a uniform logical foundation for Artificial Intelligence, as well as an abstract description of the “laws of thought” followed by the human mind. Different from “mathematical” logic, where the focus is the regularity required when demonstrating mathematical conclusions, Non-Axiomatic Logic is an attempt to return to the original aim of logic, that is, to formulate the regularity in actual human thinking. To achieve this goal, the logic is designed under the assumption that the system has insufficient knowledge and resources with respect to the problems to be solved, so that the “logical conclusions” are only valid with respect to the available knowledge and resources. Reasoning processes according to this logic covers cognitive functions like learning, planning, decision making, problem solving, etc.

This book is written for researchers and students in Artificial Intelligence and Cognitive Science, and can be used as a textbook for courses at graduate level, or upper-level undergraduate, on Non-Axiomatic Logic.

Contents:

• Introduction
• IL-1: Idealized Situation
• NAL-1: Basic Syntax and Semantics
• NAL-1: Basic Inference Rules
• NARS: Basic Memory and Control
• NAL-2: Derivative Copulas
• NAL-3: Set-Theoretic Terms
• NAL-4: Relational Terms
• NAL-5: Statements as Terms
• NAL-6: Variable Terms
• NAL-7: Events as Statements
• NAL-8: Operations and Goals as Events
• NAL-9: Self-Monitoring and Self-Control
• Summary and Beyond

Readership: Students and professionals interested in the field of artificial intelligence and machine learning.

CHAPTER 2

IL–1: IDEALIZED SITUATION

Since the existing logic systems are mostly designed for axiomatic systems, establishing NAL on AIKR is not a trivial job. We will see in the following that none of the major components of classical logic can be accepted into NAL in its current form. To simplify the design and analysis of NAL, we start from an idealized situation, where AIKR can be temporarily ignored.

In this chapter, we introduce an Inheritance Logic, or IL [Wang (1994b)]. IL is an idealized version of NAL, in the sense that it is similar to NAL in grammar, semantics, and inference rules, though it assumes sufficient knowledge and resources. Therefore, IL is not a “non–axiomatic” logic, but a step in building such a logic. Just like NAL, IL is also built with layers. For each layer

the corresponding

is defined first, then the effect of insufficient knowledge and resources is introduced, to turn

into

This chapter defines IL–1, the simplest inheritance logic.¹

In the history of logic, there are two major traditions: a “term logic” tradition exemplified by Aristotle (1882) and Sommers (1982), and a “predicate logic” tradition exemplified by Frege (1999) and Whitehead and Russell (1910). Though at the present time the latter is the dominating paradigm, NAL and IL belong to the former. The reasons of this important decision will be gradually explained in the following chapters.

2.1. Categorical Language

The simplest sentence in a predicate logic has a “predicate–arguments” format, such as P(a₁,..., a_n), where P is the predicate symbol, while each a_i

is an argument of the predicate. On the contrary, the simplest sentence in a term logic has a “subject–copula–predicate” format, which is often called a “categorical sentence”, and a language consisting of such sentences is called a “categorical language”. Since term logic uses this type of language, it is sometimes called “categorical logic” [Smith (2012)].

Narsese is a categorical language, and IL uses a version of it. The smallest component of the language is a “term”, which, in its simpest form, is an identifier used in the logic.²

Definition 2.1. The basic form of a term is a word, that is, a string of characters from a finite alphabet.

There is no additional requirement on the alphabet. In this book, the alphabet includes English letters, digits 0 to 9, and a few special signs, such as hyphen (‘–’). In the examples, we often use common English nouns for terms, such as bird and animal, just to make the examples easy to understand. There is no problem to do the same in a different natural language, such as Chinese. On the other hand, it is also fine to use terms that are meaningless to human beings, such as drib and aminal.

Definition 2.2. The basic form of a statement is an inheritance statement,

where S is the subject term, P is the predicate term, and

is the inheritance copula, defined as being a reflexive and transitive relation from one term to another term.

Graphically, an inheritance statement can be represented as two vertices connected by a directed edge. Its direction is purely conventional, though usually it is taken to be from the subject to the predicate.

The intuitive meaning of

is “S is a special case of P” or “P is a general case of S”. For example, “Bird is a type of animal” can be represented in Narsese as

Now we begin to see the difference between IL, as a term logic, and a predicate logic, like FOPL (First–Order Predicate Logic). The same example is typically represented in FOPL as a proposition

where predicates Bird and Animal both take variable x as argument, and

is the implication operator defined in propositional logic.³ Though the IL statement and the FOPL proposition have similar meanings, they are based on different ontological presumptions. FOPL presumes objects (represented by arguments) with properties and relations (represented by predicates), while IL presumes categories (represented by terms) within a generalization hierarchy (established by inheritance). One consequence of this difference is that in FOPL “predicates” and “arguments” are disjoint sets, while in IL (and NAL) “subject term” and “predicate term” are defined relatively, with respect to a certain statement, in the sense that the subject term of a statement (like the “bird” in “bird → animal”) can be the predicate term of another statement (like “dove → bird”), which is also the case in other term logics, such as Aristotle’s Syllogistic. Therefore, the “predicate symbol” in FOPL and the “predicate term” in IL are not the same, though they are intuitively related to each other.

We can also compare IL with set theory, where the above example can be represented as “Bird

Animal” with Bird and Animal being sets. Since the subset relation is both reflexive and transitive,

Table 2.1. The grammar rules of IL–1.

it is just like the inheritance relation. Here the difference is that inheritance is defined between two terms, which are not sets in general. For example, “Water is a type of liquid” that can be similarly represented in IL as “water → liquid”, though the two terms cannot be naturally considered as sets. More differences between term and set will be introduced later.

The representation language used in IL–1 contains inheritance statements as sentences, as defined by the grammar rules in Table 2.1. All grammar rules in this book are represented using a variant of the Backus Naur Form (BNF) specified in Appendix A.

2.2. Experience–Grounded Semantics

The semantic theory of IL–1 defines the truth–value of a statement, as well as the meaning of a term.

Definition 2.3. The truth–value of a statement in IL is either true or false.

Therefore, IL is a binary logic, like most of the existing logic systems.

From the relevant definitions, some theorems can be proved, as conclusions about IL.⁴ The proofs of the theorems in this book are collected in Appendix D. The following theorems directly come from the reflexivity and transitivity of the inheritance copula.

Theorem 2.1. For any term X, statement

is true.

Following the tradition of logic, such a statement is called a tautology.

Theorem 2.2. For any term X, Y, and Z, if both “X →Y ” and “Y → Z” are true, so is “X → Z”.

Treating an IL statement as a proposition, the above theorems can be expressed in FOPL as

The inheritance relation is neither symmetric nor anti–symmetric. That is, for different X and Y, given “X → Y” alone, the truth–value o...

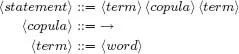
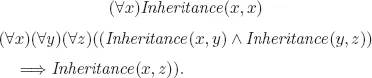
Table of contents

• Cover
• NON – AXIOMATIC LOGIC
• NON – AXIOMATIC LOGIC
• Copyright
• Dedication
• Preface
• Acknowledgments
• List of Tables
• Introduction
• IL-1: Idealized Situation
• NAL-1: Basic Syntax and Semantics
• NAL-1: Basic Inference Rules
• NARS: Basic Memory and Control
• NAL-2: Derivative Copulas
• NAL-3: Set-Theoretic Terms
• NAL-4: Relational Terms
• NAL-5: Statements as Terms
• NAL-6: Variable Terms
• NAL-7: Events as Statements
• NAL-8: Operations and Goals as Events
• NAL-9: Self-Monitoring and Self-Control
• Summary and Beyond
• Narsese Grammar
• NAL Inference Rules
• NAL Truth-Value Functions
• Proofs of Theorems
• Bibliography
• Index