Theory Of Multiple Zeta Values With Applications In Combinatorics, The

Minking Eie

• Publisher: WSPC
• Year: 2013
• Print ISBN: 9789814472630
• eBook ISBN: 9789814472654
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

This is the first book on the theory of multiple zeta values since its birth around 1994. Readers will find that the shuffle products of multiple zeta values are applied to complicated counting problems in combinatorics, and numerous interesting identities are produced that are ready to be used. This will provide a powerful tool to deal with problems in multiple zeta values, both in evaluations and shuffle relations. The volume will benefit graduate students doing research in number theory.

Contents:

• Basic Theory of Multiple Zeta Values:
  • The Time Before Multiple Zeta Values
  • Introduction to the Theory of Multiple Zeta Values
  • The Sum Formula
• Shuffle Relations among Multiple Zeta Values:
  • Some Shuffle Relations
  • Euler Decomposition Theorem
  • Multiple Zeta Values of Height Two
• Applications of Shuffle Relations in Combinatorics:
  • Generalizations of Pascal Identity
  • Combinatorial Identities of Convolution Type
  • Vector Version of Some Combinatorial Identities
• Appendices:
  • Singular Modular Forms on the Exceptional Domain
  • Shuffle Product Formulas of Multiple Zeta Values
  • The Sum Formula and Their Generalizations

Readership: Graduate students and researchers in number theory.

CHAPTER 1

Introduction to the Theory of Multiple Zeta Values

Multiple zeta values are multi-version of the classical Euler double sums

which are problems proposed by Goldbach in 1742 in an attempt to evaluate S_p,_q in terms of single zeta values, the special values at positive integers of the Riemann zeta function

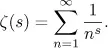
With Drinfeld integral representation of multiple zeta values, we are able to express some particular multiple zeta values or sum of multiple zeta values as integrals over simplices of two dimension, so that shuffle products of multiple zeta values can be carry out more efficiently.

1.1Introduction and Notations

For an r-tuple of positive integers α = (α₁,α₂,..., α_r) with α_r ≥ 2, the multiple zeta value or r-fold Euler sum ζ (α) [6, 5, 21, 31] is defined as

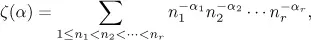
or in free dummy variables as

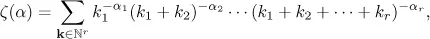
or in traditional nested form as

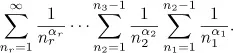
The numbers r and |α| = α₁ + α₂ + · · · + α_r are the depth and the weight of ζ (α), respectively.

The case r = 2 went back to 1742 as a problem proposed by Goldbach to Euler. For a pair of positive integers p, q with q ≥ 2, the classical Euler double sum [2, 3, 7, 10] is defined as

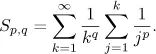
The purpose of the problem is to evaluate S_p,_q in terms of the special values at positive integers of the Riemann zeta function (or single zeta values) defined by

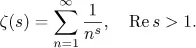
For our convenience, we let {1}^k be the k repetitions of 1, or more general, let {a}^k be the k repetitions of a. For instance, we have

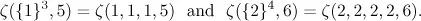
Some important results concerning multiple zeta values are worth mentioned here.

1. C. Markett [26] in 1994: Theevaluationof ζ(1,1,n).

C. Markett and later J. M. Borwein and R. Girgensohn [3...

Table of contents

• Front Cover
• Half Title
• Monographs in Number Theory
• Title Page
• Copyright
• Contents
• Preface
• I Basic Theory of Multiple Zeta Values
• 0 The Time Before Multiple Zeta Values
• 1 Introduction to the Theory of Multiple Zeta Values
• 2 The Sum Formula
• II Shuffle Relations among Multiple Zeta Values
• 3 Some Shuffle Relations
• 4 Euler Decomposition Theorem
• 5 Multiple Zeta Values of Height Two
• III Applications of Shuffle Relations in Combinatorics
• 6 Generalizations of Pascal Identity
• 7 Combinatorial Identities of Convolution Type
• 8 Vector Versions of Some Combinatorial Identities
• Appendices
• A Singular Modular Forms on the Exceptional Domain
• B Shuffle Product Formulas of Multiple Zeta Values
• C The Sum Formula and Their Generalizations
• Bibliography
• Index