Functional Equations On Groups

Henrik Stetkær

• Publisher: WSPC
• Year: 2013
• eBook ISBN: 9789814513142
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

This volume provides an accessible and coherent introduction to some of the scientific progress on functional equations on groups in the last two decades. It presents the latest methods of treating the topic and contains new and transparent proofs. Its scope extends from the classical functional equations on the real line to those on groups, in particular, non-abelian groups. This volume presents, in careful detail, a number of illustrative examples like the cosine equation on the Heisenberg group and on the group SL(2, ℝ). Some of the examples are not even seen in existing monographs. Thus, it is an essential source of reference for further investigations.

Contents:

• Introduction
• Around the Additive Cauchy Equation
• The Multiplicative Cauchy Equation
• Addition and Subtraction Formulas
• Levi–Civita's Functional Equation
• The Symmetrized Sine Addition Formula
• Equations with Symmetric Right Hand Side
• The Pre-d'Alembert Functional Equation
• D'Alembert's Functional Equation
• D'Alembert's Long Functional Equation
• Wilson's Functional Equation
• Jensen's Functional Equation
• The Quadratic Functional Equation
• K -Spherical Functions
• The Sine Functional Equation
• The Cocycle Equation
• Appendices:
  • Basic Terminology and Results
  • Substitutes for Commutativity
  • The Casorati Determinant
  • Regularity
  • Matrix-Coefficients of Representations
  • The Small Dimension Lemma
  • Group Cohomology

Readership: Advanced undergraduates, graduates and professional mathematicians interested in harmonic analysis and/or functional equations.
Key Features:

• Solutions for previously insoluble problems
• Nontrivial behavior for scalar fields
• Novel quantization procedures

Chapter 1

Introduction

1.1 A first glimpse at functional equations

A functional equation is an equation in which the unknown or unknowns are functions. To avoid a too extensive theory differential, difference and integral equations are not counted as parts of functional equations, these theories being huge separate subjects with their own own life and their own special methods.

The present book concentrates on special types of functional equations: Trigonometrical functional equations on groups, i.e., equations that extend and generalize classical relations among the trigonometric and hyperbolic functions. So our point of departure is formulas of elementary trigonometry. To take an example, the function cosine satisfies the identity

We seek the functions g :

→

that satisfy the corresponding functional equation (called d’Alembert’s functional equation or the cosine equation)

in which we have replaced cos in the identity by g. To solve (1.1) is to find all functions g :

→

for which (1.1) holds. The equation is a functional equation, because its solutions g are functions, not numbers. Incidentally, the cosine equation has other solutions than g = cos, for instance g = cosh.

Another important functional equation that we shall study, is the sine addition equation

where both f :

→

and g :

→

are unknown functions that we want to determine. So here the functional equation contains two unknown functions, not just one. The ordered pair f = sin, g = cos is a solution of (1.2), because

but this pair is not the only solution. We find all solutions in Chapter 4.

The distance function (or rather the square of it) f(x) : = ||x||² on

ⁿ satisfies the parallelogram identity

The functional equation (1.3) is called the quadratic functional equation.

The examples above show that some of the functional equations are linear, while others involve products, so we study not just linear functional equations.

We are not satisfied with finding the functions on

and

ⁿ that satisfy the classical functional equations above: We want a deeper understanding and to see the functional equations in a wider context, so we extend the scope by replacing the domain of definition

(or

ⁿ) of the functions by a group G, and instead of the classical range space

we take

or sometimes even just an abelian group. Thus given a group G we want to describe the solutions g : G →

of the cosine equation

and to find common properties of the solutions on various types of groups (like abelian or compact groups). Similarly for the sine addition formula (1.2) that takes the form

where f, g : G →

are the unknowns, and for the quadratic functional equation (1.3) that becomes becomes

with f : G →

to be found. We shall study the solutions of these and other functional equations on groups in which the group composition rule and the form of the functional equation are intertwined like in the examples above. The equations are simple to formulate, but not always to solve. The above examples are not the only ones, but are meant to give a first impression and a starting point. It turns out, as could be expected, that the composition of the set of solutions of the functional equations depends much on the structure of the group, for instance of whether it is abelian. The equations have in the special case of the abelian group G =

attracted the attention of a number of mathematicians during t...

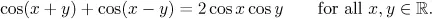
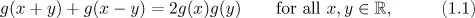
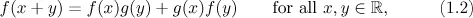
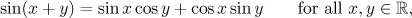
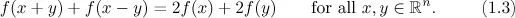
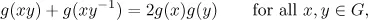
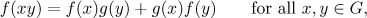
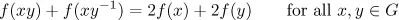
Table of contents

• Cover
• Halftitle
• Title Page
• Copyright Page
• Preface
• Contents
• 1. Introduction
• 2. Around the Additive Cauchy Equation
• 3. The Multiplicative Cauchy Equation
• 4. Addition and Subtraction Formulas
• 5. Levi-Civita’s Functional Equation
• 6. The Symmetrized Sine Addition Formula
• 7. Equations with Symmetric Right Hand Side
• 8. The Pre-d’Alembert Functional Equation
• 9. D’Alembert’s Functional Equation
• 10. D’Alembert’s Long Functional Equation
• 11. Wilson’s Functional Equation
• 12. Jensen’s Functional Equation
• 13. The Quadratic Functional Equation
• 14. K-Spherical Functions
• 15. The Sine Functional Equation
• 16. The Cocycle Equation
• Appendices