Vibration Of Piezoelectric Crystal Plates

Jiashi Yang

• Publisher: WSPC
• Year: 2013
• Print ISBN: 9789814449847
• eBook ISBN: 9789814449861
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

The first contemporary text specializing on the dynamic problems of piezoelectric crystal plates for resonant acoustic wave devices (such as resonators, filters, and sensors) since H F Tiersten's publication in 1969. This book provides an up-to-date, systematic and comprehensive presentation of theoretical results on waves and vibrations in quartz crystal plates. It expounds on the application of the theories of elasticity and piezoelectricity in acoustic wave devices made from crystal plates through a coverage spanning from classical results on acoustic wave resonators, up to present-day applications in acoustic wave sensors.

This text begins with the exposition of the simplest thickness modes and various frequency effects in them due to electrodes, mass loading, contact with fluids, air gaps, etc., and continues on to the more complicated shear-horizontal modes, as well as straight-crested modes varying along the digonal axis of rotated Y-cut quartz. Modes varying in both of the in-plane directions of crystal plates are also addressed.

The analysis within are based on the three-dimensional theories of piezoelectricity and anisotropic elasticity with various approximations when needed. Both free vibration modes (stationary waves) and propagating waves are studied in this text. Forced vibration is also treated in a few places.

This book is intended to serve as an informative reference to personnel who employ piezoelectric crystal plates in the course of their profession.

Contents:

• Theory of Piezoelectricity
• Thickness Modes in Plates: Elastic Analysis
• Thickness Modes in Plates: Piezoelectric Analysis
• Shear-horizontal Waves in Unbounded Plates
• Shear-horizontal Vibrations of Finite Plates
• Waves Propagating along Digonal Axis
• Vibration of Rectangular Plates
• Scalar Equation for Thickness Modes

Readership: Professional engineers working with Piezoelectric Crystal Plates.

Chapter 1

Theory of Piezoelectricity

This chapter presents a brief summary of the basic theory of linear piezoelectricity based mainly on the IEEE Standard on Piezoelectricity [1] and the classical book on piezoelectricity [2] by H.F. Tiersten (who also wrote the theoretical part of [1]). The same basic equations and other aspects of the theory can also be found in Chap. 2 of An Introduction to the Theory of Piezoelectricity [3]. Most of the results in this chapter are general theoretical results — only Section 1.4 has an example. Solutions to specific problems are systematically given in later chapters. This chapter uses the Cartesian tensor notation, the summation convention for repeated tensor indices, and the convention that a comma followed by an index denotes partial differentiation with respect to the coordinate associated with the index. A superimposed dot represents a time derivative.

1.1. Basic Equations

The equations of linear piezoelectricity can be obtained by linearizing the nonlinear electroelastic equations [4] under the assumption of infinitesimal deformation and fields. The resulting equations of motion and the charge equation of electrostatics are

where T is the stress tensor, ρ is the mass density, f is the body force per unit volume, u is the displacement vector, D is the electric displacement vector, and q is the body free charge density. In this book, f and q are usually zero. Constitutive relations are given by an electric enthalpy function H defined by

through

where the strain tensor, S, and the electric field vector, E, are related to the displacement, u, and the electric potential, ϕ, by

and

are the elastic, piezoelectric, and dielectric constants. The superscript, E, in

indicates that the independent electric constitutive variable is the electric field, E. The superscript, S, in

indicates that the mechanical constitutive variable is the strain tensor, S. The material constants have the following symmetries:

We also assume that the elastic and dielectric tensors are positive definite in the following sense:

Similar to Eq. (1.3), linear constitutive relations can also be written as

With successive substitutions from Eqs. (1.3) and (1.4), Eq. (1.1) can be written as four equations for u and ϕ

where we have neglected the superscripts of the material constants.

Let the region occupied by a piezoelectric body be V and its boundary surface be S, as shown in Fig. 1.1. Let the unit outward normal of S be n.

Fig. 1.1. A piezoelectric body and partitions of its surface.

For boundary conditions, we consider the following partitions of S:

where S_u is the part of S on which the mechanical displacement is prescribed, and S_T is the part of S where the traction vector is prescrib...

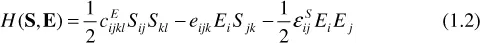
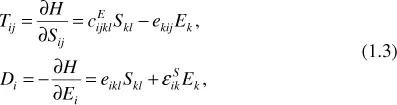
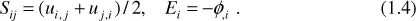
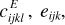
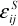
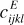
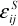
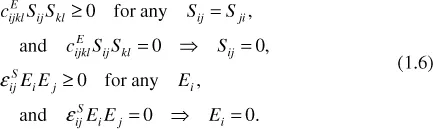
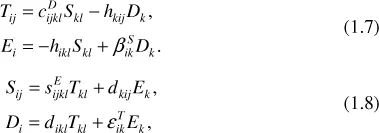
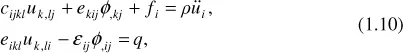
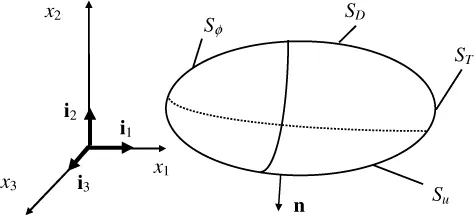
Table of contents

• Cover
• Half Title
• Title
• Copyright
• Preface
• Contents
• Chapter 1: Theory of Piezoelectricity
• Chapter 2: Thickness Modes in Plates: Elastic Analysis
• Chapter 3: Thickness Modes in Plates: Piezoelectric Analysis
• Chapter 4: Shear-horizontal Waves in Unbounded Plates
• Chapter 5: Shear-horizontal Vibrations of Finite Plates
• Chapter 6: Waves Propagating along Digonal Axis
• Chapter 7: Vibration of Rectangular Plates
• Chapter 8: Scalar Equation for Thickness Modes
• Appendix 1 Notation
• Appendix 2 Material Constants
• References
• Index