Computational Methods for Two-Phase Flow and Particle Transport

Wen Ho Lee

• Publisher: WSPC
• Year: 2013
• Print ISBN: 9789814460279
• eBook ISBN: 9789814460293
• Topic: Technology & Engineering
• Subtopic: Fluid Mechanics
• Index: Technology & Engineering

This book describes mathematical formulations and computational methods for solving two-phase flow problems with a computer code that calculates thermal hydraulic problems related to light water and fast breeder reactors. The physical model also handles the particle and gas flow problems that arise from coal gasification and fluidized beds. The second part of this book deals with the computational methods for particle transport.

Contents:

• Introduction
• Differential Equations of the Two-Phase Flow System
• Finite Differences of the Governing Equations
• A Pressure Iteration Scheme for Two-Phase Flow Modeling
• Pollution Particle Transport
• Nuclear Fission
• Radiation Hydrodynamics
• Natural Convection between Two Heated Vertical Plates
• Appendices:
  • The Two-Phase Flow Computer Code
  • Photon Transport
  • Charge Particle Transport
  • Neutron Transport

Readership: Undergraduate and graduate students studying mechanical engineering; professionals dealing with fluid mechanics, nuclear physics, and plasma physics in their day-to-day encounters — particularly the use of two-phase flows, and particle transport. Key Features:

• The only book on the market that provides a comprehensive working computer code for simulating two-phase flow problems
• Provides a comprehensive discussion on the physics of the imploding process for the inertial confinement fusion capsule surrounded by a uniform pressure field
• Detailed discussion on the variable Eddington approximation, discrete ordinates, and Monte Carlo methods for solving photon transport equations. A standard multi-group discretization of Fokker–Planck–Boltzmann equation is calculated including Coulombscattering and nuclear reactions for charge particle transport

Chapter 8

Natural Convection between Two Heated Vertical Plates

Notations

a	constant given by Eq. (8.14)
A	constant given by Eq. (8.14)
B	constant given by Eq. (8.15)
b	constant given by Eq. (8.15)
Cp, Cp0	specific heat at constant pressure ( )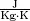
d	characteristic length (m)
g	acceleration of gravity (m/sec^2)
h	heat transfer coefficient ( )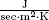
k	heat conduction coefficient ( )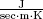
M	number of grid spacing in the X-direction (no unit)
m	ratio of the horizontal length of the barriers to the width of the channel (see Fig. 8.2)
N	number of grid spacing in the Y -direction (no unit)
n	ratio of the vertical length of the barriers to the length of the plate (see Fig. 8.2)
Nu	Nusselt number, defined by 2hd/k
NGr	Grashof number, defined by gβ(Tw − T0)(2d)^3/ν^2 where ν is the kinematic viscosity
NPr	Prandtl number, defined by μCp/k
NRa	Rayleigh number, defined by NRa = NGrNPr
P	dimensionless pressure deviation, defined by P′(2d)^2/(ρν^2) where ν is the kinematic viscosity
P′	the deviation of local pressure from the static pressure (N/m^2)
q	heat flux (W/m^2)
r	the ratio of (ΔX)^2/(ΔY )^2
T	temperature (K)
T0	static temperature (K)
Tw	temperature of the plate (K)
t	time (sec)
U	dimensionless velocity in the X-direction
u	velocity in the x-direction (m/sec)
V	dimensionless velocity in the Y-direction
v	velocity in the y-direction (m/sec), or, specific volume
w	ratio of the height to the width of channel formed by plates
X	squeezed vertical coordinate
x	dimensionless vertical coordinate, measured upwards from the middle point of the inlet section
Y	squeezed horizontal coordinate
y	dimensionless horizontal coordinate, measured upwards from the middle point of the inlet section
Z	dimensionless vorticity, defined by 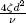where ν is the kinematic viscosity

Greek letters

α	X-direction “frequency” appearing in a Fourier expansion
β	Y-direction “frequency” appearing in a Fourier expansion, or, volume coefficient of thermal expansion (1/K)
γ	relaxation factor used in the SOR method
ΔX	grid spacing in the X-direction, defined by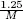
ΔY	grid spacing in the Y-direction, defined by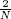
Δt	time increment
∇^2	Laplacian operator given by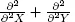
ζ	vorticity (1/sec)
θ	temperature
Θ	dimensionless temperature, defined by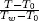
μ, μ0	dynamic viscosity ( )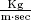
ν, ν0	kinematic viscosity (m^2/sec)
ρ, ρ0	density ( )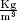
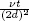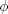τ	dimensionless time, defined by where ν is the kinematic viscosity
	some arbitrary function of x
Ψ	dimensionless stream function, defined by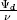
Ψd	stream function

Superscripts

′	refers to a deviation from an initial condition, or, to a value at the end ...

Table of contents

• Cover
• SemiTitle
• Title
• Copyrights
• Dedication
• Preface
• Content
• Chapter 01
• Chapter 02
• Chapter 03
• Chapter 04
• Chapter 05
• Chapter 06
• Chapter 07
• Chapter 08
• Appendix A
• Appendix B
• Appendix C
• Appendix D
• Index