
Kernel Smoothing In Matlab: Theory And Practice Of Kernel Smoothing
Theory and Practice of Kernel Smoothing
- 244 pages
- English
- ePUB (mobile friendly)
- Available on iOS & Android
Kernel Smoothing In Matlab: Theory And Practice Of Kernel Smoothing
Theory and Practice of Kernel Smoothing
About this book
Methods of kernel estimates represent one of the most effective nonparametric smoothing techniques. These methods are simple to understand and they possess very good statistical properties. This book provides a concise and comprehensive overview of statistical theory and in addition, emphasis is given to the implementation of presented methods in Matlab. All created programs are included in a special toolbox which is an integral part of the book. This toolbox contains many Matlab scripts useful for kernel smoothing of density, cumulative distribution function, regression function, hazard function, indices of quality and bivariate density. Specifically, methods for choosing a choice of the optimal bandwidth and a special procedure for simultaneous choice of the bandwidth, the kernel and its order are implemented. The toolbox is divided into six parts according to the chapters of the book.
All scripts are included in a user interface and it is easy to manipulate with this interface. Each chapter of the book contains a detailed help for the related part of the toolbox too. This book is intended for newcomers to the field of smoothing techniques and would also be appropriate for a wide audience: advanced graduate, PhD students and researchers from both the statistical science and interface disciplines.
Contents:
- Introduction
- Univariate Kernel Density Estimation
- Kernel Estimation of a Distribution Function
- Kernel Estimation and Reliability Assessment
- Kernel Estimation of a Hazard Function
- Kernel Estimation of a Regression Function
- Multivariate Kernel Density Estimation
Readership: Advanced graduate students, researchers in mathematics or statistics.
Frequently asked questions
- Essential is ideal for learners and professionals who enjoy exploring a wide range of subjects. Access the Essential Library with 800,000+ trusted titles and best-sellers across business, personal growth, and the humanities. Includes unlimited reading time and Standard Read Aloud voice.
- Complete: Perfect for advanced learners and researchers needing full, unrestricted access. Unlock 1.4M+ books across hundreds of subjects, including academic and specialized titles. The Complete Plan also includes advanced features like Premium Read Aloud and Research Assistant.
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Information
Chapter 1
Introduction
1.1 Kernels and their properties
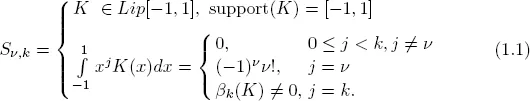 | (1.1) |
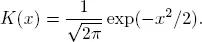
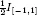


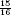
Table of contents
- Cover
- Halftitle
- Title
- Copyright
- Dedication
- Preface
- Contents
- Chapter 1: Introduction
- Chapter 2: Univariate kernel density estimation
- Chapter 3: Kernel estimation of a distribution function
- Chapter 4: Kernel estimation and reliability assessment
- Chapter 5: Kernel estimation of a hazard function
- Chapter 6: Kernel estimation of a regression function
- Chapter 7: Multivariate kernel density estimation
- Notation
- Bibliography
- Index