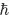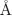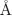Theory of Quantitative Magnetic Resonance Imaging

Hernán Jara

• Publisher: WSPC
• Year: 2013
• Print ISBN: 9789814295239
• eBook ISBN: 9789814518383
• Topic: Medicine
• Subtopic: Diagnostics Imaging

qMRI is a rapidly evolving scientific field of high current interest because it has the potential of radically changing the clinical and research practices of magnetic resonance imaging (MRI). This focuses solely on the theoretical aspects of qMRI, which are treated and analyzed at three different spatial scales, specifically: i) the quantum physics scale of individual spins; ii) the semi-classical physics scale of spin packets; and iii) the imaging scale of voxels. Topics are presented paying particular attention to theoretical unification and mathematical uniformity.

Contents:

• Introduction
• Elements of Imaging Theory
• Physics of Quantitative MRI
• Elements of Relaxation Theory
• QMRI Theory
• QMRI Processing
• Introduction to Applications of QMRI

Readership: Graduate students in physics and biomedical engineering disciplines, engineers and practitioners in biomedical engineering, MRI equipments and image processing industry.

C. PHYSICS OF QUANTITATIVE MRI

C1. Introduction

This chapter is concerned with the theoretical physics platform of qMRI, from pure quantum mechanics for describing individual ¹H-protons in water molecules, to the semi-classical description of the magnetization vector at the spin packet level via statistical mechanics, and finally to the voxel scale via imaging theory, as discussed in the previous chapter.

C1.1. The Different Spatial Scales of qMRI Theory

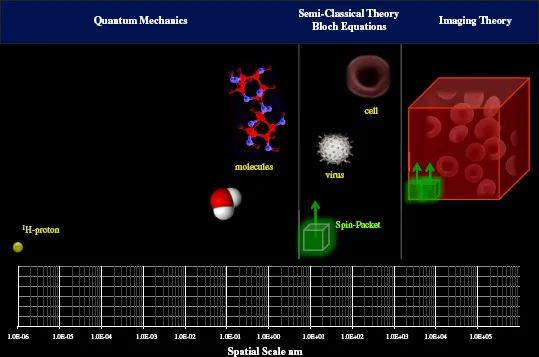
Altogether, the theoretical framework of qMRI theory deals with spatial scales spanning about twelve orders of magnitude. Starting from ¹H-protons at a spatial scale of 10^–6 nm, to that of the water molecule at a spatial scale of 10^–1 nm, to the somewhat undefined spatial scale of spin packets of ~10nm, and finally to the spatial scale of an imaging voxel, by current clinical standards of less than 10⁶ nm (<1mm).

The main objective of this chapter is to lay out the equations of motion that are valid at each one of these spatial scale regimes, progressively from smallest, to intermediate, and finally to the imaging scale where qMRI image processing takes place. Particular effort is devoted at providing logical theoretical transitions from one spatial regime to the next by analyzing selected physical systems that constitute the building blocks for the next scale and by using mathematical notations that are intuitive and consistent among spatial scales. Particular attention is given to the study of the equations of motion for a solitary ¹H-proton in a time dependent magnetic field, which are very similar to the Bloch equations and therefore are particularly useful for modeling the relaxation times in terms of microscopic randomly fluctuating magnetic fields, as discussed in Chapter D.

Fig. C-1. The physical theories and the spatial scales of MRI: From ¹H-protons, to water molecules and macromolecules, to spin packets, and finally to imaging voxels.

C1.2. The Spatial Scale of the ¹H Proton and the Water Molecule

Protons are stable spin-1/2 particles with a charge radius of approximately 0.875 10^–15m and possess a magnetic moment of 2.79 nuclear magnetons (µN = e

/2m_p = 5.050 10^–27 JT^–1). This high magnetic moment as well as the high ¹H-proton abundance in biological tissue, makes it uniquely useful for MRI in general and consequently for qMRI.

Quantum mechanics is necessary for describing ¹H-protons, water molecules, and macromolecules. One can transition to semi-classical physics for the description of spin packets and voxels.

The water's molecular geometry can be environment dependent; quoting Chaplin (Chaplin, 2010): “The experimental values for the gaseous water molecule are O-H length 0.95718

, H-O-H angle 104.474°. These values are not equal in liquid water, where ab initio calculations (O-H length 0.991

, H-O-H angle 105.5°) and neutron diffraction studies (O-H length 0.970

, H-O-H angle 106°) suggest slightly greater values, which result from hydrogen bonding weakening the covalent bonding. These bond lengths and angles are likely to change, due to polarization shifts, in different hydrogen-bonded environments and when the water molecules are bound to solutes and ions.”

We can calculate the intra-molecular proton-to-proton distance to be 1.55

using the neutron diffraction values (O-H length 0.970

, H-O-H angle 106°) and the triangle formula:

The inter-molecular proton-to-proton closest distance of approach can be derived from published results of ab initio calculations as twice the longitudinal van der Waals radius of hydrogen in the water molecule, specifically 2.4

. Although evidence exist that the water molecule is not perfectly spherical with about a ±5% variation in van der Waals diameter, here we assumed molecular sphericity and a van der Waals radius of 1.7

. This value can be chosen for simulations because it is intermediate between the published minimum and maximum values of 1.6

and 1.8

respectively. We can assume to a first approximation that the shape and dimensions of water are the same in pure liquid water as in biological tissues. In other words, we can assume that water's electronic configuration does not change significantly due to interactions with the biological microenvironment.

C1.3. Spin Packets

The spatial scale of spin packets is somewhat ambiguously defined; on one hand, the semi-classical NMR theory requires spin packets to be much larger than the water molecule so that number of contained spins is sufficiently large and the laws of statistical mechanics apply for describing the packet's spin state populations. On the other hand, the theory also calls for submicroscopic spin packets so that the magnetization distribution inside the patient as well as inside the imaging voxels can be modeled as a continuous function of space and time, thus enabling theory formulation in terms of partial differential equations. In a crude model, we can imagine spin packets as small cubes containing about 10^{4 1}H-protons in order to fully guarantee the appropriateness of the statistical mechanics description. Considering that the water molecule di...

Table of contents

• Cover Page
• Title Page
• Copyright Page
• Dedication Page
• Contents
• Preface
• A. Introduction
• B. Elements of Imaging Theory
• C. Physics of Quantitative MRI
• D. Elements of Relaxation Theory
• E. qMRI Theory
• F. qMRI Processing
• G. Introduction to Applications of qMRI