Lecture Notes On Mathematical Olympiad Courses: For Junior Section (In 2 Volumes) - Volume 2

For Junior SectionVolume 2

Jiagu Xu

• Publisher: WSPC
• Year: 2009
• Print ISBN: 9789814293532
• eBook ISBN: 9789814365208
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

Olympiad mathematics is not a collection of techniques of solving mathematical problems but a system for advancing mathematical education.

This book is based on the lecture notes of the mathematical Olympiad training courses conducted by the author in Singapore. Its scope and depth not only covers and exceeds the usual syllabus, but introduces a variety concepts and methods in modern mathematics.

In each lecture, the concepts, theories and methods are taken as the core. The examples are served to explain and enrich their intension and to indicate their applications. Besides, appropriate number of test questions is available for reader's practice and testing purpose. Their detailed solutions are also conveniently provided.

The examples are not very complicated so that readers can easily understand. There are many real competition questions included which students can use to verify their abilities. These test questions are from many countries, e.g. China, Russia, USA, Singapore, etc. In particular, the reader can find many questions from China, if he is interested in understanding mathematical Olympiad in China.

This book serves as a useful textbook of mathematical Olympiad courses, or as a reference book for related teachers and researchers.

Contents

• Volume 2:
  • Congruence of Integers
  • Decimal Representation of Integers
  • Pigeonhole Principle
  • Linear Inequality and System of Linear Inequalities
  • Inequalities with Absolute Values
  • Geometric Inequalities
  • Solutions to Testing Questions
• and other chapters

Readership: Mathematics students, school teachers, college lecturers, university professors; mathematics enthusiasts.

Solutions to Testing Questions

Solutions to Testing Questions

Solutions to Testing Questions 16

Testing Questions (16-A)

1.

, so the answer is (A).

2.

3.

4.

5.

6.

from

7.

c < b < a.

8. We have

.since

9. Let

then,

10. Since U, V, W > 0, it is sufficient to compare U², V², W². From

Therefore U² > V² > W², i.e. W < V < U.

Testing Questions (16-B)

1. Considering negative number cannot be under square root sign, we find |a| = 3, i.e. a = ±3. Further, 3 − a appears in denominator implies a = 3, so a = −3. Thus

Thus, the units digit of x is 6 since any positive integer power of 6 always has units digit 6.

2. Let

, then the given expression becomes

3. More general, we calculate

Now n = 1998, so

.

4. Given

, find the value of

.

From

so that

Thus,

5. We find [M] first. Let

. Then M = A⁶ and

, AB = 2, so

Since M = A⁶, for finding [M], we now consider A⁶ + B⁶:

which is an integer.

yields 0 < B⁶ < 1, so [M] = A⁶ + B⁶ − 1 and

Thus,

Solutions to Testing Questions 17

Testing Questions (17-A)

1.

2.

3.

4. Let

, then a² + b² = 16, ab = 1, so

5. Let

, then a² + b² = 8, ab = 3, so

6.

7. Since

, so

8. Let

, where a, b, c > 0. By taking squares to both sides, then

Thus,

.

9. Let

, then

.

It's clear that a ≥ 1. When

,< 2, i.e. 1 ≤ a < 5, then

. When 5 ≤ a, then

Thus,

10. It is clear that

. On the other hand,

Thus, A is the root of the given equation for x.

Testing Questions (17-B)

1. It is clear that ab > 0, i.e. a and b have same signs. Let

, then

if a = 0 and b < 0; or

if b = 0 and a < 0.

A is not defined if a > 0, b > 0 since

.

Thus,

if A is defined.

3. Since

therefore

4. Let

, then y ≥ 0 and

, so that

5.

yields

, so

...

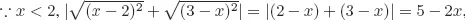
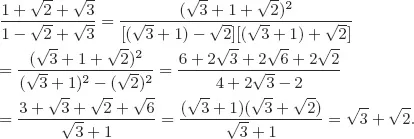
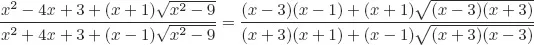
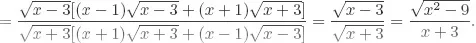
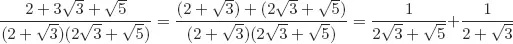
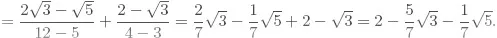
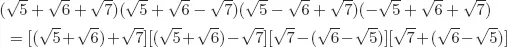
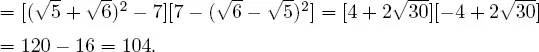
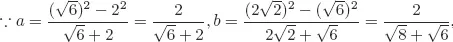
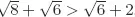
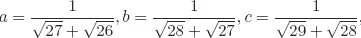
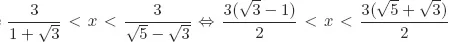
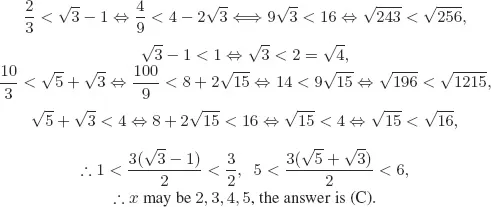
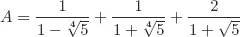
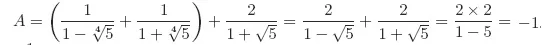
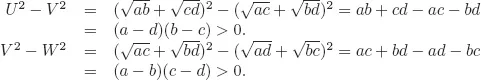
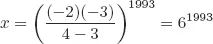
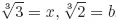
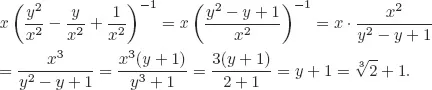
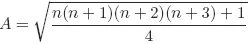
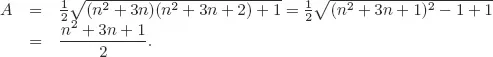
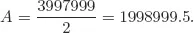
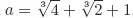
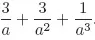
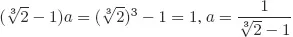
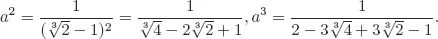
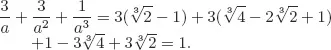
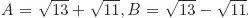
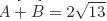
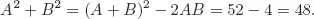
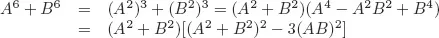
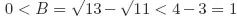
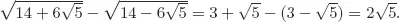
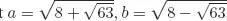
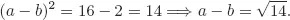
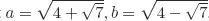
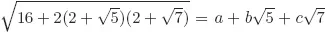
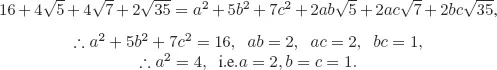
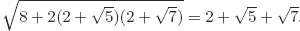
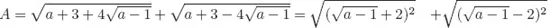
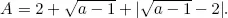
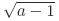
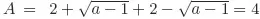
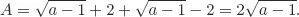
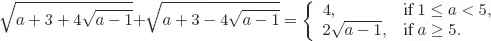
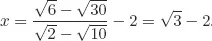
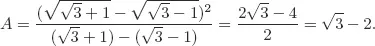
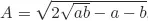
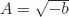
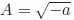
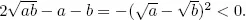
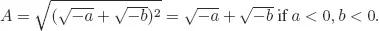
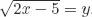
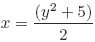
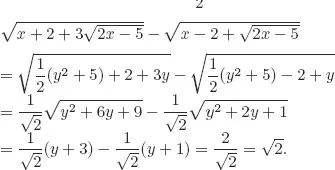
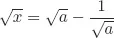
Table of contents

• Cover Page
• Title Page
• Copyright Page
• Preface
• Acknowledgments
• Abbreviations and Notations
• Contents
• 16. Quadratic Surd Expressions and Their Operations
• 17. Compound Quadratic Surd Form
• 18. Congruence of Integers
• 19. Decimal Representation of Integers
• 20. Perfect Square Numbers
• 21. Pigeonhole Principle
• 22. [x] and {x}
• 23. Diophantine Equations (I)
• 24. Roots and Discriminant of Quadratic Equation
• 25. Relation between Roots and Coefficients of Quadratic Equations
• 26. Diophantine Equations (II)
• 27. Linear Inequality and System of Linear Inequalities
• 28. Quadratic Inequalities and Fractional Inequalities
• 29. Inequalities with Absolute Values
• 30. Geometric Inequalities
• Solutions to Testing Questions
• Index