A Course in Linear Algebra with Applications

2nd Edition

Derek J S Robinson

• Publisher: WSPC
• Year: 2006
• Print ISBN: 9789812700247
• eBook ISBN: 9789814365444
• Edition: 2
• Topic: Mathematics
• Subtopic: Linear Algebra
• Index: Mathematics

This is the second edition of the best-selling introduction to linear algebra. Presupposing no knowledge beyond calculus, it provides a thorough treatment of all the basic concepts, such as vector space, linear transformation and inner product. The concept of a quotient space is introduced and related to solutions of linear system of equations, and a simplified treatment of Jordan normal form is given.

Numerous applications of linear algebra are described, including systems of linear recurrence relations, systems of linear differential equations, Markov processes, and the Method of Least Squares. An entirely new chapter on linear programing introduces the reader to the simplex algorithm with emphasis on understanding the theory behind it.

The book is addressed to students who wish to learn linear algebra, as well as to professionals who need to use the methods of the subject in their own fields.

Contents:

• Matrix Algebra
• Systems of Linear Equations
• Determinants
• Introduction to Vector Spaces
• Basis and Dimension
• Linear Transformations
• Orthogonality in Vector Spaces
• Eigenvectors and Eigenvalues
• More Advanced Topics
• Linear Programming

Readership: Undergraduates in mathematics, engineering, physics and information science; scientists who need to use linear algebra.

Chapter One

MATRIX ALGEBRA

In this first chapter we shall introduce one of the principal objects of study in linear algebra, a matrix or rectangular array of numbers, together with the standard matrix operations. Matrices are encountered frequently in many areas of mathematics, engineering, and the physical and social sciences, typically when data is given in tabular form. But perhaps the most familiar situation in which matrices arise is in the solution of systems of linear equations.

1.1 Matrices

An m × matrix A is a rectangular array of numbers, real or complex, with m rows and n columns. We shall write ciij for thenumber that appears in the ith row and the jth column of A; this is called the (i,j) entry of A. We can either write A in the extended form

or in the more compact form

Thus in the compact form a formula for the (i,j) entry of A is given inside the round brackets, while the subscripts m and n tell us the respective numbers of rows and columns of A.

Explicit examples of matrices are

Example 1.1.1

Write down the extended form of the matrix

.

The (i, j) entry of the matrix is (—l)^lj + i where i — 1, 2, 3, and j — 1,2. So the matrix is

It is necessary to decide when two matrices A and B are to be regarded as equal; in symbols A = B. Let us agree this will mean that the matrices A and B have the same numbers of rows and columns, and that, for all i and j, the (i,j) entry of A equals the (i,j) entry of B. In short, two matrices are equal if they look exactly alike.

As has already been mentioned, matrices arise when one has to deal with linear equations. We shall now explain how this comes about. Suppose we have a set of m linear equations in n unknowns

. These may be written in the form

Here the a_ij and are to be regarded as given numbers. The problem is to solve the system, that is, to find all n-tuples of numbers

that satisfy every equation of the system, or to show that no such numbers exist. Solving a set of linear equations is in many ways the most basic problem of linear algebra.

The reader will probably have noticed that there is a matrix involved in the above linear system, namely the coefficient matrix

In fact there is a second matrix present; it is obtained by using the numbers bi, b2,…, b_m to add a new column, the (n + l)th, to the coefficient matrix A. This results in an m x (n + 1) matrix called the augmented matnx of the linear system. The problem of solving linear systems will be taken up in earnest in Chapter Two, where it will emerge that the coefficient and augmented matrices play a critical role. At this point we merely wish to point out that here is a natural problem in which matrices are involved in an essential way.

Example 1.1.2

The coefficient and augmented matrices of the pair of linear equations

are respectively

Some special matrices

Certain special types of matrices that occur frequently will now be recorded.

(i) A 1 × n matrix, or — row vector, A has a single row

(ii) An m × 1 matrix, or m-column vector, B has just one column

(iii) A matrix with the same number of rows and columns is said to be square.

(iv) A zero matrix is a matrix all of whose entries are zero. The zero m × n matrix is denoted by

Sometimes 0_nn is written 0_n. For example, O23 is the matrix

(v) The identity nxn matrix has l's on the principal diagonal, that is, from top left to bottom right, and zeros elsewhere; thus it has the form

This matrix is written

The identity matrix plays the role of the number 1 in matrix multiplication.

(vi) A square matrix is called upper triangular if it has only zero entries below the principal diagonal. Similarly a matrix

is lower triangular if all entries above the principal diagonal are zero. For example, the matrices

are upper triangular and lower triangular respectively.

(vii) A square matrix in which all the non-zero elements lie on the principal diagonal is called a diagonal matrix. A scalar matrix is a diagonal matrix in which the elements on the principal diagonal are all equal. For example, the matrices

are respectively diagonal and scalar. Diagonal matrices have much simple...

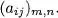
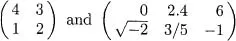
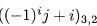
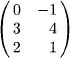
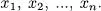
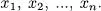
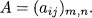
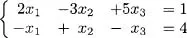
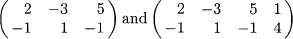
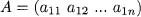
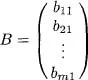
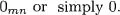
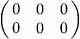
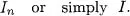
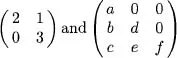
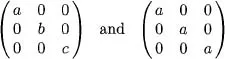
Table of contents

• Cover Page
• Title Page
• Copyright Page
• Contents
• Preface to the Second Edition
• Preface to the First Edition
• Chapter One Matrix Algebra
• Chapter Two Systems of Linear Equations
• Chapter Three Determinants
• Chapter Four Introduction to Vector Spaces
• Chapter Five Basis and Dimension
• Chapter Six Linear Transformations
• Chapter Seven Orthogonality in Vector Spaces
• Chapter Eight Eigenvectors and Eigenvalues
• Chapter Nine More Advanced Topics
• Chapter Ten Linear Programming
• Appendix Mathematical Induction
• Answers to the Exercises
• Bibliography
• Index
• Back Cover