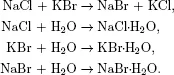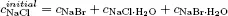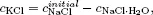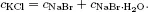Chemical Thermodynamics

With Examples for Nonequilibrium Processes

Byung Chan Eu, Mazen Al-Ghoul

• Publisher: WSPC
• Year: 2010
• ISBN:
  9789814365185
• Topic: Sciences biologiques
• Subtopic: Biochimie

Thermodynamics is an ever evolving subject. This book aims to introduce to advanced undergraduate students and graduate students the fundamental ideas and notions of the first and second laws of thermodynamics in a manner unavailable in the usual textbooks on the subject of thermodynamics. For example, it treats the notions of unavailable work, compensated and uncompensated heats, and dissipation, which make it possible to formulate the thermodynamic laws in more broadened forms than those in the conventional treatment of equilibrium thermodynamics. It thus strives to prepare students for more advanced subjects of irreversible processes, which are encountered in our everyday scientific activities. In addition, it also aims to provide them with functional and practical knowledge of equilibrium chemical thermodynamics of reversible processes in real fluids. It discusses temperature, work and heat, thermodynamic laws, equilibrium conditions and thermodynamic stability, thermodynamics of reversible processes in gases and liquids, in surfaces, chemical equilibria, reversible processes in electrolyte solutions and dielectrics in static electric and magnetic fields. A couple of examples for irreversible processes associated with fluid flows and chemical pattern formation and wave propagations are discussed as examples for applications of broader treatments of the thermodynamic laws in the realm of irreversible phenomena.

Contents:

• Introduction
• Temperature, Work, and Heat
• The First Law of Thermodynamics
• The Second Law of Thermodynamics
• Equilibrium Conditions and Thermodynamic Stability
• The Third Law of Thermodynamics
• Thermodynamics of Mixtures and Open Systems
• Heterogeneous Equilibria
• Thermodynamics of Real Fluids
• Canonical Equation of State
• Thermodynamics of Real Gas Mixtures
• Chemical Equilibria
• Thermodynamics of Solutions
• Thermodynamics of Surfaces
• Electrolyte Solutions
• Debye–Hückel Theory of Strong Electrolyte Solutions
• Galvanic Cells and Electromotive Forces
• Thermodynamics of Electric and Magnetic Fields
• Thermodynamics of Nonequilibrium Processes
• Appendices
  • Local Form of Energy Conservation Law
  • Various Coefficients Used in Chapter 10

Readership: Suitable as a chemistry textbook for undergraduates and graduates and also as a reference source to physical chemistry researchers and chemical engineers.

Chapter 1

Introduction

Thermodynamics in the generalized sense is a branch of natural science in which we study heat, work, energy, their interrelationships, and the modes by which systems exchange heat, matter, and energy with each other and with the surroundings, by converting heat into work, and vice versa. Since all human activities and natural phenomena involve matter and energy of one form or another, the importance of such science is obvious, and for that reason it is in the foundations of physical, biological, and engineering sciences. As a matter of fact, thermodynamics owes its genesis to the urgent need at the early stage of the Industrial Revolution in the first half of the 19th century, to understand how steam engines work and improve their efficiencies, since the efficiencies of such engines had significant economic implications then. Such questions are still relevant even to this day in our everyday economic and industrial activities. On one hand, such a need motivated scientists and engineers to study the properties of steam in particular and gases in general to construct, for example, the steam table. On the other hand, it culminated in the idealization of engines with a reversible cycle by S. Carnot, who made a lasting contribution through his penetrating analysis of how heat engines operate, and his study resulted in his famous principle now known as Carnot's theorem (although his analysis was based on the caloric theory of heat which was proven to be an incorrect notion of heat). Later pioneers such as R. Clausius and W. Thomson (Lord Kelvin) adopted the correct notion of heat—in which heat is regarded as a form of energy—and developed a theory by retaining truthful features in Carnot's exposition and expanding on it. Through their efforts and the works by subsequent researchers, the science of thermodynamics was born in the second half of the 19th century. The subject was refined, especially in an important way, by J. W. Gibbs through his well-known work on heterogeneous equilibria. The modern form of the science of thermodynamics, laid on the foundations shaped by efforts by S. Carnot, Count Rumford (Benjamin Thompson), J. R. Mayer, R. Clausius, W. Thomson, H. Helmholtz, and J. W. Gibbs among others, has been developed by numerous other researchers, but its applications to chemical and chemical engineering problems owe a great deal to the works by M. Planck, W. Nernst, F. Haber, and G. N. Lewis and his school to name a few. The works of Max Born and C. Caratheodory have given equilibrium thermodynamics another mathematical aspect through Caratheodory's theorem, which opens up a geometrical viewpoint to thermodynamics. However, we will not discuss this line of thoughts in this work.

It is now generally believed that all natural macroscopic phenomena occur in full conformation to the laws governing thermodynamics. Although the subject of thermodynamics has been around over 160 years by now, it is not closed, since the pioneers in thermodynamics limited the development to reversible processes and thus to systems in equilibrium, it is still an open, developing science. It is therefore worth a serious study, especially since irreversible phenomena are not sufficiently well understood as yet from the standpoint of the laws of thermodynamics, especially if irreversible processes occur far removed from equilibrium.

From the viewpoint of thermodynamics of irreversible processes, equilibrium thermodynamics—which, more precisely, should be called thermostatics and we are going to study it here—is merely dealing with systems at a singular state of thermodynamic equilibrium. Since there are no macroscopically discernable processes occurring in equilibrium systems, equilibrium thermodynamics deals with idealized reversible processes and thus is not capable of describing what is happening in the real system over a finite time span and over space; rather, it is only able to tell us the possibilities of that particular event as far as the laws of thermodynamics are concerned. The description of the process over a finite span of time and space is in the realm of irreversible thermodynamics, which is still in the developing stage at present. The basic reason that the subject of equilibrium thermodynamics is useful and powerful despite the idealized reversible processes studied in it is that some macroscopic thermodynamic properties of a system which is going through irreversible processes can be related to the complementary quantities computed from the reversible processes, as will be shown later when we delve into the subject. This is because there is a state function of thermodynamic state variables for the system even if the processes are irreversible. This state function extends the notion of the equilibrium entropy into the domain of irreversible processes. The existence of such a state function—called calortropy—lifts thermodynamics from the level of studying only idealized reversible processes, as in equilibrium thermodynamics, to a level of using a more insightful and powerful mathematical tool for studying various aspects of irreversible behavior of the system. We will elaborate on this point in the chapters dealing with the second law of thermodynamics.

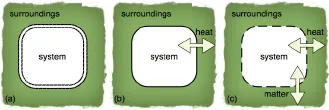
Since we are going to use various terms in our study, we fix their meanings by introducing the following system of terminology. A system is that part of the physical world which is under consideration, and the rest of the physical world is called the surroundings. When a system exchanges mass, heat, work, and any other forms of energy with the surroundings, it is called an open system (c). When a system does not exchange matter but energies with the surroundings, it is said to be a closed system (b). If a system has no interaction whatsoever with the surroundings, it is called an isolated system (a) (Fig. 1.1). It is possible to regard the system and the surroundings together as an isolated system. We will find it convenient to do so for some cases.

Thermodynamics is concerned with gross observables of a macroscopic system and their interrelationships. Since according to the atomic theory of matter a macroscopic system consists of an enormous number of atoms and molecules not counting elementary subnuclear particles, a microscopic description of the macroscopic system would entail knowledge of an enormous number of microscopic variables. However, a large number of molecules in an assembly exhibit as a rule a collective behavior, which may be described by a small number of variables called macroscopic variables or macroscopic coordinates. A macroscopic variable (coordinate) is an observable whose determination requires only measurements, over long time spans compared with periods of thermal motion, that take averages of microscopic variables over regions containing a large number of molecules, and involving large energies compared with individual energies of atoms and molecules. Pressure, volume, temperature, and internal energy, are examples of such macroscopic variables.

Fig. 1.1 The system and surroundings—universe. Panel (a) is an isolated system; (b) is a closed system; (c) is an open system.

We often speak of thermodynamic properties. These are termed as the properties of the system which describe its macroscopic coordinates. Thermodynamic properties are classified into two categories. If a thermodynamic property is independent of the mass of the system, then it is called an intensive property. Examples are pressure, temperature, concentrations, and molar properties. If a thermodynamic property depends on the mass of the system, it is called an extensive property. Examples are the volume, energy, and entropy of a system which increase in proportion to the mass of the system. Intensive and extensive properties (variables) often appear as conjugate pairs of variables in thermodynamics. We may take the examples of pressure and volume, and temperature and entropy for such conjugate pairs of thermodynamic variables. Intensive properties, however, may vary with position in the space as do the extensive variables, if the system is not homogeneous. If the intensive properties are continuous functions of position throughout the system, then the system is called homogeneous, and if they are not continuous functions of position throughout the system, then the system is called heterogeneous. For example, a system is heterogeneous if the density changes discontinuously across the boundary of two homogeneous regions of the system. Such homogeneous regions of a heterogeneous system are called the phases of the system. An example for heterogeneous systems is a system of water and ice, and in this particular case there are two phases in the system.

We will often speak of a thermodynamic state. The thermodynamic state of a system is defined by its intensive properties. They may or may not change over space and time. A system is said to be in a state of thermodynamic equilibrium if (a) the thermodynamic state of the system does not change in the time duration of the observation performed; and (b) no material or energy flux exists in its interior or at the boundaries with the surroundings. Otherwise, the system is in a state of nonequilibrium. In thermodynamics we examine systems which are in a state of thermodynamic equilibrium.

A system may be composed of a single component or more than one component. In the former case, the system is called a pure system and in the latter case, it is called a mixed system or simply a mixture. In a mixture there may arise the question as to the number of independent components of the system: it is defined by the minimum number of chemical species from which the system can be prepared in each phase of the system by a specified set of physicochemical procedures. A practical way of determining the number of independent components is the total number of components minus the number of distinct chemical and other restrictive conditions such as chemical reactions and charge neutrality conditions. For example, consider a system formed when NaCl, KBr, and H₂O are mixed. If KCl, NaBr, NaBr·H₂O, KBr·H₂O, and NaCl·H₂O are isolated on chemical analysis, the distinct chemical reactions are

If the concentration of species i is denoted by c_i, and since the relations for the concentrations are

and

where c_NaCI^initial is the initial concentration of NaCl, we find

This means that the number of independent components is (8–1)–4 = 3 in this case.

In Chapter 2 of this work, the notions of temperature, work, and heat are discussed. In Chapter 3, the first law of thermodynamics is discussed together with thermochemistry, which deals with measurements of heat released or absorbed by the system. In Chapter 4, the second law of thermodynamics is discussed. This important principle, which was literally enunciated by Lord Kelvin and R. Clausius, was given a mathematical representation in the form of inequality now known as the Clausius inequality. In this work, the Clausius inequality will be replaced by an equation as a general mathematical representation of the second law of thermodynamics, which remains valid even if there are irreversible processes present in the system. The said mathematical representation of the second law of thermodynamics permits us to develop the thermodynamics of irreversible processes in a general context. For this purpose we introduce the notion of calortropy. This part of the treatment of the second law of thermodynamics sets the present work apart from the conventional methods used in other works available in the literature on thermodynamics. The distinctive point of the new quantity is that it is the extension to nonequilibrium of the notion of equilibrium entropy that was originally introduced by Clausius for reversible processes only. By the accomplished extension, we are now provided with the starting point of a theory of irreversible processes in a general form, and even the equilibrium thermodynamics of Clausius is provided with a window through which we can glimpse into the world of irreversible phenomena, even if one studies just the reversible process associated with the irreversible process in question. The nonequilibrium extension of the Clausius entropy is given the new term calortropy, which means heat evolution. This extension frees us from the shackles of entropy defined for equilibrium only, and equilibrium thermodynamics consequently becomes easier to comprehend than otherwise.

In the rest of the book, we treat the conventional subjects of equilibrium thermodynamics, which are commonly discussed in courses on thermodynamics. The subjects covered are thermodynamics of gases, liquids, and solutions; heterogeneous equilibria; chemical equilibria; strong electrolytes; galvanic cells; and the Debye-Hückel theory of strong electrolytes, which is the only concession we make to discuss a statistical treatment of macroscopic phenomena. We will also discuss the thermodynamics of systems subject to electromagnetic fields and the thermodynamics of interfacial phenomena. In the last chapter, we discuss a couple of examples of application of irreversible processes, which are treated in the formalism developed for the notion of calortropy and the attendant macroscopic theory of irreversible processes. This chapter is meant to introduce the reader to the subject of irreversible phenomena.

We believe that thermodynamics is a subject that should be studied without intrusion by a molecular theory approach, because it is a subject that allows us to make deductions with regard to macroscopic properties of matter without reference to the molecular picture of matter, and eventually serves as the ultimate aim of molecular theory of macroscopic matter, which is developed by means of statistical mechanics. Mixing thermodynamics and statistical mechanics tends to confuse important issues vis à vis thermodynamics, which are involved in the statistical mechanical treatment of macroscopic properties of matter, and such possible confusion would hinder a logical development of the theory of irreversible processes. However, a concession is made for the pedagogical importance of the Debye–Hückel theory indispensable in the physical chemistry of electrolytes and plasmas, including the theory of electrolytic conductance.

A major portion of this book is based on the materials taught by B. C. Eu in the courses on thermodynamics, off and on, over a period of over two decades at McGill University. The same materials have been taught by M. Al-Ghoul at American University of Beirut for a couple of terms.

Chapter 2

Temperature, Work, and Heat

Temperature, work, and heat are three basic concepts underlying the science of thermodynamics, the scientific quantification of which traces back to the very beginning of thermodynamics. Feeling hot or cold is a physiological sensation that we have when we touch an object, but such sensation was not given an objective measure until the times of Galileo. Furthermore, the relation of temperature to heat and the relation of work to heat have evolved through the history of science, their evolution embodying our struggle to understand their nature. In this chapter, we discuss their quantification, so that they can be made use of in the subsequent study of thermodynamics in a scientific and logical manner.

2.1 Temperature

Temperature is not only one of the most impor...