Geometry Of Crystallographic Groups

Andrzej Szczepański

• Publisher: WSPC
• Year: 2012
• Print ISBN: 9789814412254
• eBook ISBN: 9789814412278
• Topic: Biowissenschaften
• Subtopic: Wissenschaft Allgemein

Crystallographic groups are groups which act in a nice way and via isometries on some n -dimensional Euclidean space. They got their name, because in three dimensions they occur as the symmetry groups of a crystal (which we imagine to extend to infinity in all directions). The book is divided into two parts. In the first part, the basic theory of crystallographic groups is developed from the very beginning, while in the second part, more advanced and more recent topics are discussed. So the first part of the book should be usable as a textbook, while the second part is more interesting to researchers in the field. There are short introductions to the theme before every chapter. At the end of this book is a list of conjectures and open problems. Moreover there are three appendices. The last one gives an example of the torsion free crystallographic group with a trivial center and a trivial outer automorphism group.

This volume omits topics about generalization of crystallographic groups to nilpotent or solvable world and classical crystallography.

We want to emphasize that most theorems and facts presented in the second part are from the last two decades. This is after the book of L Charlap “Bieberbach groups and flat manifolds” was published.

Contents:

• Definitions
• Bieberbach Theorems
• Classification Methods
• Flat Manifolds with b 1 = 0
• Outer Automorphism Groups
• Spin Structures and Dirac Operator
• Flat Manifolds with Complex Structures
• Crystallographic Groups as Isometries of ℍ n
• Hantzsche–Wendt Groups
• Open Problems

Readership: Researchers in geometry and topology, algebra and number theory and chemist.

Chapter 1

Definitions

In this introductory chapter we define a language of the isometry group of the Euclidean space. We also introduce an elementary world of covering spaces, group actions and discrete subgroups.

Let

ⁿ be an n-dimensional Euclidean space with the standard scalar product

where

and

This gives us a norm of vectors

and metric

Definition 1.1. A map

is an isometry if for any

The next proposition follows directly from the definition.

Proposition 1.1. The set of all isometries of

ⁿ is a group with respect to composition of maps.

By E(n) we shall denote the group of all isometries of the Euclidean space

ⁿ. We distinguish two types of isometries: translations and linear orthogonal maps.

Definition 1.2. Let a ∈

ⁿ. A map

defined by the formula

t_a (x) = a + x

is called a translation of the space

ⁿ.

Proposition 1.2. The set of all translations of

ⁿ is a normal subgroup of E(n). The function a → t_a defines an isomorphism of the additive group

ⁿ and the group of all translations of

ⁿ.

Therefore, we shall also denote by

ⁿ the group of all translations of the Euclidean space

ⁿ.

Definition 1.3. A linear map :

is orthogonal if for any x,y ∈

ⁿ

Proposition 1.3. A linear map

is orthogonal if and only if for any x ∈

ⁿ,

x

=

A(x)

.

Proof. The implication ‘⇒’ follows from the definition of the orthogonal map. For the proof of the other implication let us assume that A is a ...

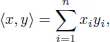
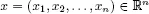
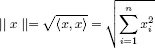
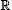
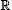
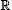
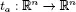
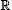
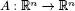
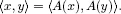
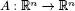
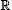
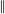
Table of contents

• Cover
• HalfTitle
• SubTitle
• Title
• Copyright
• Preface
• Contents
• 1. Definitions
• 2. Bieberbach Theorems
• 3. Classification Methods
• 4. Flat Manifolds with b1 = 0
• 5. Outer Automorphism Groups
• 6. Spin Structures and Dirac Operator
• 7. Flat Manifolds with Complex Structures
• 8. Crystallographic Groups as Isometries of Rn
• 9. Hantzsche-Wendt Groups
• 10. Open Problems
• Appendix A Alternative Proof of Bieberbach Theorem
• Appendix B Burnside Transfer Theorem
• Appendix C Example of a Flat Manifold without Symmetry
• Bibliography
• Index