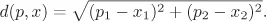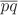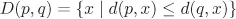Voronoi Diagrams and Delaunay Triangulations

Franz Aurenhammer, Rolf Klein, Der-Tsai Lee

• Publisher: WSPC
• Year: 2013
• Print ISBN: 9789814447638
• eBook ISBN: 9789814447652
• Topic: Matemáticas
• Subtopic: Algoritmos de programación

Voronoi diagrams partition space according to the influence certain sites exert on their environment. Since the 17th century, such structures play an important role in many areas like Astronomy, Physics, Chemistry, Biology, Ecology, Economics, Mathematics and Computer Science. They help to describe zones of political influence, to determine the hospital nearest to an accident site, to compute collision-free paths for mobile robots, to reconstruct curves and surfaces from sample points, to refine triangular meshes, and to design location strategies for competing markets.

This unique book offers a state-of-the-art view of Voronoi diagrams and their structure, and it provides efficient algorithms towards their computation.

Readers with an entry-level background in algorithms can enjoy a guided tour of gently increasing difficulty through a fascinating area. Lecturers might find this volume a welcome source for their courses on computational geometry. Experts are offered a broader view, including many alternative solutions, and up-to-date references to the existing literature; they might benefit in their own research or application development.

Contents:

• Introduction
• Elementary Properties
• Basic Algorithms
• Advanced Properties
• Generalized Sites
• Higher Dimensions
• General Spaces & Distances
• Applications and Relatives
• Miscellanea
• Alternative Solutions in R d
• Conclusions

Readership: Students of mathematics and computer science, scientists and engineers working in mathematics, natural sciences and economics.

Chapter 1

INTRODUCTION

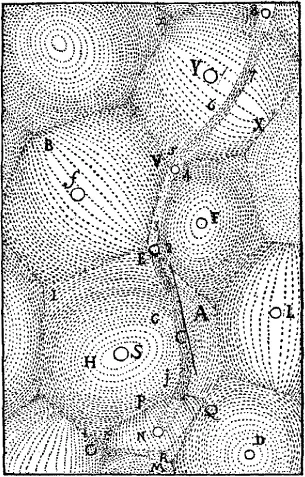
This book is devoted to an important and influential geometrical structure called the Voronoi diagram, whose origins in the Western literature date back to at least the 17th century. In his work on the principles of philosophy [257], René Descartes (Renatus Cartesius) claims that the solar system consists of vortices. His illustrations show a decomposition of space into convex regions, each consisting of matter revolving around one of the fixed stars; see Figure 1.1.

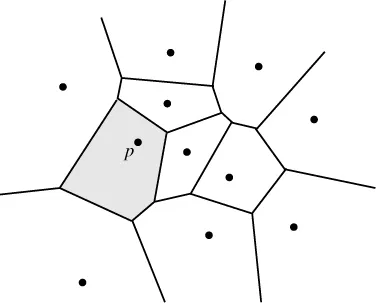
Even though Descartes has not explicitly defined the extension of these regions, the underlying idea seems to be the following. Let some space, and a set of sites in this space be given, together with a notion of the influence a site p exerts on every location x of the space. Then the region of the site p consists of all points x for which the influence of p is the strongest. Figure 1.2 illustrates the simplest case: Sites are points in the plane, and influence is modeled by Euclidean distance. The regions of the sites are convex polygons covering the entire plane.

‘The world is full of Voronoi diagrams’ ... this phrase seems true wherever we look, and it is the intention of this book to lead the reader into the fascinating realm of Voronoi diagrams. Whether we look to the sky, where gravitational fields structure the macrocosmos, or consider the spread of animals in their habitats, simply watch the interference pattern of waves on a quiet pond, or even peer deep within the structure of matter, we will find a Voronoi diagram-like pattern which structures the world.

Indeed, this fundamental concept has emerged independently, and proven useful, in various fields of science. Most applications have their own notions of ‘space’, ‘sites’, and ‘influence’, resulting in Voronoi diagrams whose structures differ greatly. Understanding their properties is the key to their effective application and to the development of fast construction algorithms. Various names have been given to Voronoi diagrams, depending on the particular domain, such as Thiessen polygons in geography and meteorology (Thiessen [683], 1911), domains of action or Wirkungsbereiche in crystallography (Niggli [562], 1927), Wigner–Seitz zones in chemistry and physics (Wigner and Seitz [705], 1933), Johnson–Mehl model in mineralogy (Johnson and Mehl [433], 1939), and medial axis transform in biology and physiology (Blum [134], 1973).

Figure 1.1. Descartes’ decomposition of space into vortices.

Voronoi diagrams are important to both theory and applications, and play a unique interdisciplinary role. Several thousands of research articles have been published about them in different communities. Results thus dispersed might not always be widely known, and might fade into oblivion. While no single book can present all known results on Voronoi diagrams and their relatives, our aim is to thoroughly cover the structural and algorithmic viewpoints. In addition to being a versatile space partitioning structure, Voronoi diagrams are also aesthetically pleasing, and many people feel attracted to them, even regarding their artistic aspects. We have tried to communicate this quality in this book.

Figure 1.2. A Voronoi diagram of point sites in the Euclidean plane.

One and a half centuries ago, the mathematicians Carl Friedrich Gauß [353] (1840) and Gustav Lejeune Dirichlet [280] (1850), and later Georgi Feodosjewitsch Voronoi [693, 694] (1908) were the first to formally introduce this concept. They used it to study quadratic forms: Here the sites are integer lattice points, and influence is measured by Euclidean distance. The resulting structure was called a Dirichlet tessellation or Voronoi diagram, which became its standard name today.

Voronoi [693] also considered the geometrical dual of this structure, where any two (point) sites are connected whose regions have a boundary in common. Later, Boris Delaunay (Delone) [253] obtained the same structure by defining that two sites are connected if they lie on a circle whose interior contains no other sites. After him, the dual of the Voronoi diagram was denoted Delaunay tessellation or Delaunay triangulation.

With the advent of modern computers, the important role of Voronoi diagrams in structuring, representing, and displaying multidimensional data was rediscovered by computational geometers. Voronoi diagrams are a well-established geometric data structure nowadays. About one out of sixteen articles in computational geometry is dedicated to them, ever since Shamos and Hoey [637] introduced them to the field. In the two-dimensional case, for instance in the Euclidean plane, the Voronoi diagram does not require significantly more storage than does its underlying set of sites, and thus captures the inherent proximity information in a comprehensive and computationally useful manner. Its applications in more practically oriented areas of computer science are numerous, for example, in geographic information systems, robotics, computer graphics, and data classification and clustering, to name a few.

Besides its direct applications in diverse fields of science, the Voronoi diagram and its dual can be used for solving numerous, and surprisingly different, geometric and graph-theoretical problems. Due to their close relationship to polytopes and arrangements of hyperplanes in higher dimensions, many questions (and solutions) from convex and discrete geometry carry over to Voronoi diagrams. Moreover, the Delaunay triangulation, seen as a combinatorial graph, is related to several prominent connectivity graphs. We discuss various respective applications, often including alternative solutions for their special merits. Along the way, we give a state-of-the-art account of the literature on Voronoi diagrams in computational geometry. This fills the need for a technically sound and well-structured book, which is up-to-date on the theory and mathematical applications of Voronoi diagrams.

The reader is invited on a guided tour of gently increasing difficulty through a fascinating area. Insight will be given into the ideas and principles of Voronoi diagrams, without the baggage of too much technical detail. When later faced with a geometric partitioning problem, readers should find our book helpful in deciding whether their problem shows Voronoi characteristics and which type of Voronoi diagram applies. They might find a ready-to-use solution in our book, or follow up the links to the literature provided, or they might work out their own solution based on the algorithms they have seen. The book targets researchers in mathematics, computer science, natural and economical sciences, instructors and graduate students in those fields, as well as the ambitious engineers looking for alternative solutions. A brief discussion of algorithmic implementation questions, and of currently available geometric computation libraries, is included in the final chapter. Since human intuition is aided by visual perception, especially where geometric topics are concerned, the diversity and appeal of Voronoi diagrams is liberally illustrated with appropriate figures.

The presentation and structure of this book strives to highlight the intrinsic potential of Voronoi diagrams and Delaunay triangulations, which lies in their structural properties, in the existence of efficient algorithms for their construction, and in their relationship to seemingly unrelated concepts. We therefore organized topics by concept, rather than by application.

Another book which nicely complements ours, but from a much more applied perspective, is by Okabe et al. [571] (2000). It contains a wealth of applications of Voronoi diagrams, several of them not (or only marginally) covered here, like Poisson Voronoi diagrams and locational optimization problems. The more than one thousand and six hundred references listed in [571] constitute a bibliography still quite distinct from ours — demonstrating once more the broad scope of Voronoi diagrams. In addition, the book by Gavrilova [354] (2008) contains a collection of articles on diverse applications in the natural sciences, with numerous citations. A careful study of Delaunay triangulations, mainly oriented towards their algorithmic applications in surface meshing and finite element methods, is contained in George and Borouchaki [356] (1998). The recent book on Delaunay mesh generation by Cheng, Dey, and Shewchuk [202] (2013) takes into account the various new developments to date.

Shorter and early treatments of Voronoi diagrams and Delaunay triangulations, closer to the spirit of the present book, are the surveys by Aurenhammer [93], Fortune [343], and Aurenhammer and Klein [100]. Also, Chapters 5 and 6 of Preparata and Shamos [596], Chapter 13 of Edelsbrunner [300], Chapters 7 and 9 of de Berg et al. [244], and Part V of Boissonnat and Yvinec [151] could be consulted.

Although interesting and insightful in its own right, we decided to refrain from a detailed historical treatment of Voronoi diagrams in this book. The interested reader is encouraged to enjoy the historical perspectives presented in [93], and later in more detail, in [571].

We start in Chapter 2 with a simple case — the Voronoi diagram and the Delaunay triangulation of n points in the plane, under Euclidean distance. We state elementary structural properties that follow directly from the definitions. Further properties will be revealed in Chapter 3, where different algorithmic schemes for computing these structures are presented. In Chapter 4 we complete our presentation of the classical two-dimensional case, with advanced properties of planar Voronoi diagrams and Delaunay triangulations. We next turn to generalizations, to sites more general than points in Chapter 5, and to higher dimensions in Chapter 6. Generalized spaces and distances are treated elaborately in Chapter 7. In Chapter 8, important geometric applications of the Voronoi diagram and the Delaunay triangulation are discussed, along with respective related structures and concepts. The reader interested mainly in these applications can proceed directly to Chapter 8, after Chapter 2 or 3. Chapter 9 presents relevant topics which, for clarity of exposition, are best described separately. Chapter 10 offers alternative solutions in high dimensions, where the attractiveness of Voronoi diagrams is partially lost due to their high combinatorial and computational worst-case complexity. Finally, Chapter 11 concludes the book, gives a short discussion of algorithmic implementation issues, and mentions some important open problems.

Chapter 2

ELEMENTARY PROPERTIES

In this chapter, we present definitions and basic properties of the Voronoi diagram and its dual, the Delaunay triangulation.

Only the simplest case is considered — point sites in the plane under the Euclidean distance. Yet, the properties discussed are of general importance, as many (but not all) of them will carry over to other types of Voronoi diagrams and their relatives, presented later in this book.

2.1.Voronoi diagram

Let us start with giving some standard notation and explanations. Throughout this chapter, we will denote by S a set of n ≥ 3 point sites p, q, r,... in the Euclidean plane, R² . For points p = (p₁ , p₂ ) and x = (x₁ , x₂ ), their Euclidean distance is given as

The straight-line segment that connects two points p and q will be written as

, or sometimes just as pq.

For p, q ∈ S, let B(p, q) be the bisector of p and q (also called their separator ), which is the locus of all points in R² at equal distance from both p and q. B(p, q) is the perpendicular line through the midpoint of the line segment

. It separates the halfplane

closer to p from the halfplane D(q, p) closer to q.

We next ...

Table of contents

• Front Cover
• Half Title
• Title Page
• Copyright
• Contents
• 1. Introduction
• 2. Elementary Properties
• 3. Basic Algorithms
• 4. Advanced Properties
• 5. Generalized Sites
• 6. Higher Dimensions
• 7. General Spaces & Distances
• 8. Applications and Relatives
• 9. Miscellanea
• 10. Alternative Solutions in Rd
• 11. Conclusions
• Bibliography
• Index