Advances In The Homotopy Analysis Method

Shijun Liao

• Publisher: WSPC
• Year: 2013
• eBook ISBN: 9789814551267
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

Unlike other analytic techniques, the Homotopy Analysis Method (HAM) is independent of small/large physical parameters. Besides, it provides great freedom to choose equation type and solution expression of related linear high-order approximation equations. The HAM provides a simple way to guarantee the convergence of solution series. Such uniqueness differentiates the HAM from all other analytic approximation methods. In addition, the HAM can be applied to solve some challenging problems with high nonlinearity.This book, edited by the pioneer and founder of the HAM, describes the current advances of this powerful analytic approximation method for highly nonlinear problems. Coming from different countries and fields of research, the authors of each chapter are top experts in the HAM and its applications. Contents:

• Chance and Challenge: A Brief Review of Homotopy Analysis Method (S-J Liao)
• Predictor Homotopy Analysis Method (PHAM) (S Abbasbandy and E Shivanian)
• Spectral Homotopy Analysis Method for Nonlinear Boundary Value Problems (S Motsa and P Sibanda)
• Stability of Auxiliary Linear Operator and Convergence-Control Parameter (R A Van Gorder)
• A Convergence Condition of the Homotopy Analysis Method (M Turkyilmazoglu)
• Homotopy Analysis Method for Some Boundary Layer Flows of Nanofluids (T Hayat and M Mustafa)
• Homotopy Analysis Method for Fractional Swift–Hohenberg Equation (S Das and K Vishal)
• HAM-Based Package NOPH for Periodic Oscillations of Nonlinear Dynamic Systems (Y-P Liu)
• HAM-Based Mathematica Package BVPh 2.0 for Nonlinear Boundary Value Problems (Y-L Zhao and S-J Liao) Graduate students and researchers in applied mathematics, physics, nonlinear mechanics, engineering and finance. Key Features:
  • The method described in the book can overcome almost all restrictions of other analytic approximation method for nonlinear problems
  • This book is the first in homotopy analysis method, covering the newest advances, contributed by many top experts in different fields

Chapter 1

Chance and Challenge:
A Brief Review of Homotopy Analysis Method

Shijun Liao

Shanghai Jiao Tong University, Shanghai 200240, China
[email protected]

A brief review of the homotopy analysis method (HAM) and some of its current advances are described. We emphasize that the introduction of the homotopy, a basic concept in topology, is a milestone of the analytic approximation methods, since it is the homotopy which provides us great freedom and flexibility to choose equation type and solution expression of high-order approximation equations. Besides, the so-called “convergence-control parameter” is a milestone of the HAM, too, since it is the convergence-control parameter that provides us a convenient way to guarantee the convergence of solution series and that differs the HAM from all other analytic approximation methods. Relations of the HAM to the homotopy continuation method and other analytic approximation techniques are briefly described. Some interesting but challenging nonlinear problems are suggested to the HAM community. As pointed out by Georg Cantor (1845–1918), “the essence of mathematics lies entirely in its freedom”. Hopefully, the above-mentioned freedom and great flexibility of the HAM might create some novel ideas and inspire brave, enterprising, young researchers with stimulated imagination to attack them with satisfactory, better results.

Contents

1.1. Background

1.2. A brief history of the HAM

1.3. Some advances of the HAM

1.3.1. Generalized zeroth-order deformation equation

1.3.2. Spectral HAM and complicated auxiliary operator

1.3.3. Predictor HAM and multiple solutions

1.3.4. Convergence condition and HAM-based software

1.4. Relationships to other methods

1.5. Chance and challenge: some suggested problems

1.5.1. Periodic solutions of chaotic dynamic systems

1.5.2. Periodic orbits of Newtonian three-body problem

1.5.3. Viscous flow past a sphere

1.5.4. Viscous flow past a cylinder

1.5.5. Nonlinear water waves

References

1.1. Background

Physical experiment, numerical simulation and analytic (approximation) method are three mainstream tools to investigate nonlinear problems. Without doubt, physical experiment is always the basic approach. However, physical experiments are often expensive and time-consuming. Besides, models for physical experiments are often much smaller than the original ones, but mostly it is very hard to satisfy all similarity criterions. By means of numerical methods, nonlinear equations defined in rather complicated domain can be solved. However, it is difficult to gain numerical solutions of nonlinear problems with singularity and multiple solutions or defined in an infinity domain. By means of analytic (approximation) methods, one can investigate nonlinear problems with singularity and multiple solutions in an infinity interval, but equations should be defined in a simple enough domain. So, physical experiments, numerical simulations and analytic (approximation) methods have their inherent advantages and disadvantages. Therefore, each of them is important and useful for us to better understand nonlinear problems in science and engineering.

In general, exact, closed-form solutions of nonlinear equations are hardly obtained. Perturbation techniques [1–4] are widely used to gain analytic approximations of nonlinear equations. Using perturbation methods, many nonlinear equations are successfully solved, and lots of nonlinear phenomena are understood better. Without doubt, perturbation methods make great contribution to the development of nonlinear science. Perturbation methods are mostly based on small (or large) physical parameters, called perturbation quantity. Using small/large physical parameters, perturbation methods transfer a nonlinear equation into an infinite number of sub-problems that are mostly linear. Unfortunately, many nonlinear equations do not contain such kind of perturbation quantities at all. More importantly, perturbation approximations often quickly become invalid when the so-called perturbation quantities enlarge. In addition, perturbation techniques are so strongly dependent upon physical small parameters that we have nearly no freedom to choose equation type and solution expression of high-order approximation equations, which are often complicated and thus difficult to solve. Due to these restrictions, perturbation methods are valid mostly for weakly nonlinear problems in general.

On the other side, some non-perturbation methods were proposed long ago. The so-called “Lyapunov’s artificial small-parameter method” [5] can trace back to the famous Russian mathematician Lyapunov (1857–1918), who first rewrote a nonlinear equation

(1.1)

where r and t denote the spatial and temporal variables, u(r, t) a unknown function, f(r, t) a known function,

₀ and

₀ are linear and nonlinear operator, respectively, to such a new equation

(1.2)

where q has no physical meaning. Then, Lyapunov regarded q as a small parameter to gain perturbation approximations

(1.3)

and finally gained approximation

(1.4)

by setting q = 1, where

(1.5)

and so on. It should be emphasized that one has no freedom to choose the linear operator

₀ in Lyapunov’s artificial s...

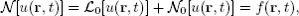
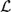
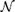
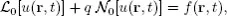
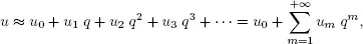
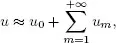
Table of contents

• Cover
• Half Title
• Title Page
• Copyright
• Preface
• Contents
• Chapter 1. Chance and Challenge: A Brief Review of Homotopy Analysis Method
• Chapter 2. Predictor Homotopy Analysis Method (PHAM)
• Chapter 3. Spectral Homotopy Analysis Method for Nonlinear Boundary Value Problems
• Chapter 4. Stability of Auxiliary Linear Operator
• Chapter 5. A Convergence Condition of the Homotopy Analysis Method
• Chapter 6. Homotopy Analysis Method for Some Boundary Layer Flows of Nanofluids
• Chapter 7. Homotopy Analysis Method for Fractional Swift–Hohenberg Equation
• Chapter 8. HAM-Based Package NOPH for Periodic Oscillations of Nonlinear Dynamic Systems
• Chapter 9. HAM-Based Mathematica Package BVPh 2.0 for Nonlinear Boundary Value Problems