Forcing For Mathematicians

Nik Weaver

• Publisher: WSPC
• Year: 2014
• eBook ISBN: 9789814566025
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

Ever since Paul Cohen's spectacular use of the forcing concept to prove the independence of the continuum hypothesis from the standard axioms of set theory, forcing has been seen by the general mathematical community as a subject of great intrinsic interest but one that is technically so forbidding that it is only accessible to specialists. In the past decade, a series of remarkable solutions to long-standing problems in C * -algebra using set-theoretic methods, many achieved by the author and his collaborators, have generated new interest in this subject. This is the first book aimed at explaining forcing to general mathematicians. It simultaneously makes the subject broadly accessible by explaining it in a clear, simple manner, and surveys advanced applications of set theory to mainstream topics.

Contents:

• Peano Arithmetic
• Zermelo–Fraenkel Set Theory
• Well-Ordered Sets
• Ordinals
• Cardinals
• Relativization
• Reflection
• Forcing Notions
• Generic Extensions
• Forcing Equality
• The Fundamental Theorem
• Forcing CH
• Forcing ¬ CH
• Families of Entire Functions*
• Self-Homeomorphisms of βℕ \ ℕ, I*
• Pure States on B ( H )*
• The Diamond Principle
• Suslin's Problem, I*
• Naimark's problem*
• A Stronger Diamond
• Whitehead's Problem, I*
• Iterated Forcing
• Martin's Axiom
• Suslin's Problem, II*
• Whitehead's Problem, II*
• The Open Coloring Axiom
• Self-Homeomorphisms of βℕ \ ℕ, II*
• Automorphisms of the Calkin Algebra, I*
• Automorphisms of the Calkin Algebra, II*
• The Multiverse Interpretation

Readership: Graduates and researchers in logic and set theory, general mathematical audience.

Chapter 1Peano Arithmetic

Forcing is a powerful technique for proving consistency and independence results in relation to axiomatic set theory. A statement is consistent with a given family of axioms if it cannot be disproven on the basis of those axioms, and independent of them if it can be neither proven nor disproven. When we have established that some assertion is consistent, there is still hope that it might actually be provable from the axioms, but once we have shown it is independent the matter is closed.

The preeminent historical example of an independent statement is Euclid’s fifth axiom, the parallel postulate:

(5) Given a line and a point not on that line, at most one line can be drawn through the given point that is parallel to the given line.

This statement is independent of the other four axioms of Euclidean geometry:

(1) A straight line can be drawn between any two points.

(2) A line segment can be extended indefinitely in both directions.

(3) A circle can be drawn with any center and any radius.

(4) All right angles are equal to each other.

How do we know this? The parallel postulate is consistent with the other four axioms because all five statements hold in the standard Euclidean plane. Its negation is consistent with the other four axioms because the first four axioms hold in a hyperbolic plane (taking “lines” to be geodesics), but the parallel postulate fails. Thus, we may assume either the parallel postulate or its negation without fear of contradiction.

No doubt the reader is already familiar to some degree with this example and is not about to raise any objections to the conclusion we just reached. But there is room for criticism. The problem is that Euclid’s “axioms” are stated in an informal manner that apparently presupposes an intuitive grasp of the flat plane they are intended to describe. In fact they hardly qualify as axioms in the modern sense. To be fair, Euclid does preface his axioms with informal “definitions” of the terms appearing in them, but several of these are also quite vague (e.g., “a line is a breadthless length”) and again presuppose some implicit knowledge of the subject matter.

Thus, there is a legitimate question as to whether it is completely clear that this implicit knowledge assumed by Euclid is compatible with the hyperbolic plane example. I do not wish to argue this point, only to emphasize the desirability of setting up a purely formal axiomatic system equipped with a precise symbolic language and well-defined rules of inference. If the system is ambiguous in any way then we cannot consider consistency and independence to be rigorous mathematical concepts.

Peano arithmetic, usually abbreviated PA, is a good example of a formal axiomatic system. It is simple enough to be described in detail. These details don’t matter so much for us, but seeing them once may help give the reader a clearer sense of the way axiomatic systems work.

The language of PA is specified as follows. We start with an infinite list of variables x, y, . . .; a constant symbol 0; symbols for the addition, multiplication, and successor operations (+, ·, ′); and parentheses. The variables are to be thought of as ranging over the natural numbers, and the successor symbol as representing the operation of adding 1. A term is any grammatical expression built up from these components, e.g., something like 0′′ + x · y′ (with parentheses omitted here for the sake of readability), and an atomic formula is a statement of the form t₁ = t₂ where t₁ and t₂ are terms. Finally, a formula is any statement built up from atomic formulas using parentheses and the logical symbols ¬ (not), → (implies), and ∀ (for all).

For the sake of economy, we can limit ourselves to these three logical symbols and regard expressions involving the symbols ∨ (or), ∧ (and), ↔ (if and only if), and ∃ (there exists) as abbreviating longer expressions involving only ¬, →, and ∀. For instance, ϕ ∨

is equivalent to ¬ϕ →

. Thus statements like “x is prime” can be rendered symbolically, say as

and then translated into a form that uses only ¬, →, and ∀. Evidently, this simple language is flexible enough to express a large variety of elementary number-theoretic assertions: every number is a sum of four squares, there is a prime pair greater than any number, etc.

The axioms of PA come in three groups. First, we have logical axioms which represent general logical truths, starting with

L1 ϕ → (

→ ϕ)

L2 [ϕ → (

→ θ)] → [(ϕ →

) → (ϕ → θ)]

L3 (¬

→ ¬ϕ) → (ϕ →

).

Properly speaking, the preceding are not axioms but axiom schemes, meaning that they are to be thought of as templates which can be used to generate infinitely many axioms by replacing ϕ,

, and θ with any formulas. Also falling under the rubric of “logical axioms” are two schemes pertaining to quantification,

L4 (∀x)(ϕ →

) → (ϕ → (∀x)

),

where ϕ and

are any formulas such that ϕ contains no unquantified appearance of x, and

L5 (∀x)ϕ(x) → ϕ(t),

where ϕ is any formula and t is any term that can be substituted for x in ϕ(x) without any of its variables becoming quantified. (This restriction on t prevents disasters like (∀x)(∃y)(y = x) → (∃y)(y = y′).)

Next, we have equality axioms which describe basic properties of equality. The axioms

E1 x = x

E2 x = y → y = x

E3 x = y → (y = z → x = z)

E4 x = y → x′ = y′

suffice here. Axioms analogous to E4 for the other operations + and · need not be added separately because they can be proven, within PA, from E4.

Finally, PA includes the non-logical axioms

(1) ¬(0 = x′)

(2) x′ = y′ → x = y

(3) x + 0 = x

(4) x + y′ = (x + y)′

(5) x · 0 = 0

(6) x · y′ = x · y + x

(7) ϕ(0) → [(∀x)(ϕ(x) → ϕ(x′)) → (∀x)ϕ(x)]

wh...

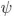
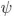
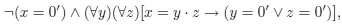
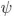
Table of contents

• Cover
• Halftitle
• Titlepage
• Copyright
• Dedication
• Contents
• Preface
• 1. Peano Arithmetic
• 2. Zermelo-Fraenkel Set Theory
• 3. Well-Ordered Sets
• 4. Ordinals
• 5. Cardinals
• 6. Relativization
• 7. Reflection
• 8. Forcing Notions
• 9. Generic Extensions
• 10. Forcing Equality
• 11. The Fundamental Theorem
• 12. Forcing CH
• 13. Forcing-CH
• 14. Families of Entire Functions*
• 15. Self-Homeomorphisms of βN \ N, I*
• 16. Pure States on B(H)*
• 17. The Diamond Principle
• 18. Suslin’s Problem, I*
• 19. Naimark’s Problem*
• 20. A Stronger Diamond
• 21. Whitehead’s Problem, I*
• 22. Iterated Forcing
• 23. Martin’s Axiom
• 24. Suslin’s Problem, II*
• 25. Whitehead’s Problem, II*
• 26. The Open Coloring Axiom
• 27. Self-Homeomorphisms of βN \ N, II*
• 28. Automorphisms of the Calkin Algebra, I*
• 29. Automorphisms of the Calkin Algebra, II*
• 30. The Multiverse Interpretation
• Appendix A Forcing with Preorders
• Exercises
• Notes
• Bibliography
• Notation Index
• Subject Index