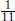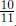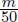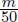Game Theory And Mechanism Design

Y Narahari

• Publisher: WSPC
• Year: 2014
• eBook ISBN: 9789814525060
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

This book offers a self-sufficient treatment of a key tool, game theory and mechanism design, to model, analyze, and solve centralized as well as decentralized design problems involving multiple autonomous agents that interact strategically in a rational and intelligent way. The contents of the book provide a sound foundation of game theory and mechanism design theory which clearly represent the “science” behind traditional as well as emerging economic applications for the society.

The importance of the discipline of game theory has been recognized through numerous Nobel prizes in economic sciences being awarded to game theorists, including the 2005, 2007, and 2012 prizes. The book distills the marvelous contributions of these and other celebrated game theorists and presents it in a way that can be easily understood even by senior undergraduate students.

A unique feature of the book is its detailed coverage of mechanism design which is the art of designing a game among strategic agents so that a social goal is realized in an equilibrium of the induced game. Another feature is a large number of illustrative examples that are representative of both classical and modern applications of game theory and mechanism design. The book also includes informative biographical sketches of game theory legends, and is specially customized to a general engineering audience.

After a thorough reading of this book, readers would be able to apply game theory and mechanism design in a principled and mature way to solve relevant problems in computer science (esp, artificial intelligence/machine learning), computer engineering, operations research, industrial engineering and microeconomics.

Contents:

• • Introduction and Overview
• Non-Cooperative Game Theory:
  • Key Notions in Game Theory
  • Extensive Form Games
  • Strategic Form Games
  • Dominant Strategy Equilibria
  • Pure Strategy Nash Equilibria
  • Mixed Strategies and Mixed Strategy Nash Equilibrium
  • Utility Theory
  • Matrix Games
  • Existence of Nash Equilibrium
  • Computation of Nash Equilibria
  • Complexity of Computing a Nash Equilibrium
  • Bayesian Games
• Mechanism Design:
  • Introduction to Mechanism Design
  • Implementation of Social Choice Functions by Mechanisms
  • Incentive Compatibility and Revelation Theorem
  • The Gibbard-Satterthwaite Impossibility Theorem
  • Vickrey-Clarke-Groves (VCG) Mechanisms
  • Mechanism Design Space in Quasilinear Environment
  • Auctions
  • Optimal Mechanisms and Myerson Auction
  • Mechanism Design for Sponsored Search Auctions
  • Implementation in Ex-Post Nash Equilibrium
  • Further Topics in Mechanism Design
• Cooperative Game Theory:
  • Correlated Strategies and Correlated Equilibrium
  • The Two Person Bargaining Problem
  • Coalitional Games with Transferable Utility
  • The Core of Coalitional Games
  • The Shapley Value
  • Other Solution Concepts in Cooperative Game Theory
  • Stable Matching
  • Epilogue
  • Mathematical Preliminaries

Readership: Senior undergraduate, first year master's, and first year research students, academics and industrial researchers in computer science, computer engineering, networks and communications, artificial intelligence/machine learning, operations research, industrial engineering, management science, and microeconomics.
Key Features:

• First of its kind to include a balanced treatment of noncooperative game theory, cooperative game theory, as well as mechanism design
• Incorporates a large number of apt, illustrative examples to facilitate an immediate and comprehensive understanding of the concepts and ideas
• Examples chosen carefully from traditional and modern topics in computer science, networks, and microeconomics
• Includes biographical sketches of leading game theorists at appropriate places

Chapter 1

Introduction and Overview

In this chapter, we bring out the importance and current relevance of game theory and mechanism design. The modern era, marked by magnificent advances in information and communication technologies, has created possibilities for fascinating new applications. In many of these applications, the research challenges can be effectively addressed using game theory and mechanism design. In this chapter, we describe a few motivational examples and present several modern research trends that have brought game theory and mechanism design to the forefront.

Game theory and mechanism design deal with interactions among strategic agents. While game theory is concerned with analysis of games, mechanism design involves designing games with desirable outcomes. Currently these are lively and active areas of research for inter-disciplinary problem solving. The central objective of this book is to gain a sound understanding of the science behind the use of game theory and mechanism design in solving modern problems in the Internet era. This book deals with three broad areas: non-cooperative game theory, cooperative game theory, and mechanism design.

Disciplines where game theory and mechanism design have traditionally been used include economics, business science, sociology, political science, biology, philosophy, and engineering. In engineering, it has been most widely used in industrial engineering, inventory management, supply chain management, electronic commerce, and multiagent systems. More recently, game theory has been embraced by computer science and electrical engineering disciplines in the context of many emerging applications.

1.1Game Theory: The Science of Strategic Interactions

The term game used in the phrase game theory corresponds to an interaction involving decision makers or players who are rational and intelligent. Informally, rationality of a player implies that the player chooses his strategies so as to maximize a well defined individualistic payoff while intelligence means that players are capable enough to compute their best strategies. Game theory is a tool for logical and mathematical analysis that models conflict as well as cooperation between the decision makers and provides a principled way of predicting the result of the interactions among the players using equilibrium analysis. Traditional games such as chess and bridge represent games of a fairly straightforward nature. Games that game theory deals with are much more general and could be viewed as abstractions and extensions of the traditional games. The abstractions and extensions are powerful enough to include all complexities and characteristics of social interactions. For this reason, game theory has proved to be an extremely valuable tool in social sciences in general and economics in particular. While game theory focuses on analysis of games, mechanism design is concerned with design of games to obtain desirable outcomes - mechanism design could be described as reverse engineering of games. In the sequel, whenever there is no need for emphasis, we use the single phrase game theory instead of the phrases game theory and mechanism design.

1	2
	IISc	MG Road
IISc	100, 100	0, 0
MG Road	0, 0	10, 10

Table 1.1: Payoffs for the students in different situations

Value of Game Theory and Mechanism Design

We provide four simple, stylized examples which bring out the value of game theory and mechanism design in modeling situations of conflict and cooperation among strategic agents. These examples are abstractions of representative real-world situations and applications.

Student Coordination Problem

Imagine two typical students (call them 1 and 2), say belonging to the Indian Institute of Science (IISc), Bangalore, who are close friends. The students derive utility by spending time together either studying (in IISc) or going to the MG Road (Mahatma Gandhi Road, a location in Bangalore, frequented by young students seeking entertainment). Thus to spend time together, they have two options (or strategies): IISc and MG Road. If both of them are in IISc, each one gets a payoff of 100. If both of them go to MG Road, each gets a payoff of only 10. If one of them remains in IISc and the other goes to MG Road, the payoff is 0 for each. The payoffs are shown in Table 1.1 and are self-explanatory. Suppose the two friends have to choose their strategies simultaneously and independently of each other. Being rational and intelligent, each one would like to select the best possible strategy. It is clear that both opting for IISc is the best possible outcome and both opting for MG Road is also fine though clearly worse than both opting for IISc. The worst happens when they choose different options since each ends up with zero utility.

Game theory helps us with a principled way of predicting the options that would be chosen by the two students. In this case, the outcome of both opting for IISc and the outcome of both opting for MG Road can be shown to be what are called Nash equilibria which are strategy profiles in which no player is better off by unilaterally deviating from her equilibrium strategy. Game theory also provides one more prediction for this game which on the face of it is counter-intuitive but represents an equilibrium outcome that the students will not be averse to playing. This outcome which is technically called a mixed strategy Nash equilibrium corresponds to the situation where each student chooses IISc with probability

and MG Road with probability

. This perhaps explains why some students are found mostly in MG Road and rarely in IISc!

The above game which is often called the coordination game is an abstraction of many social and technical situations in the real world. We will not get into details here but only leave the comment that game theory enables a scientific way of predicting the outcome of such interactions among decision makers.

Braess Paradox

We now illustrate the Braess paradox which is named after the German mathematician Dietrich Braess. This paradox is usually associated with transportation networks and brings out the counter-intuitive fact that a transportation network with extra capacity added may actually perform worse for commuters (in terms of time delays) than without the extra capacity. The game that we describe here is developed on the lines presented in the book by Easley and Kleinberg [1].

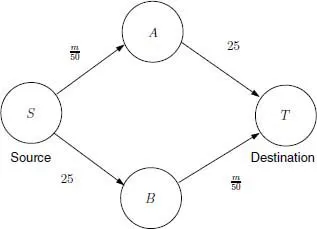
Figure 1.1 shows a network that consists of a source S and a destination T, and two intermediate hubs A and B. All vehicles traveling from S can go via hub A or hub B. Suppose, regardless of the number of vehicles on the route, it takes 25 minutes to travel from S to B or from A to T. On the other hand, the travel time from S to A is

minutes where m is the number of vehicles traveling on that link. Similarly, the travel time from B to T is

minutes where m is the number of vehicles on that link.

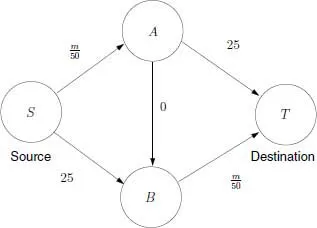
Suppose we now introduce an additional fast link from A to B to ease the congestion in the network (as a degenerate case, we will assume the travel time from A to B to be zero). Figure 1.2 depicts this new network with an extra link added from A to B. Now a vehicle can go from S to T in three different ways: (1) S to A to T; (2) S to B to T; and (3) S to A to B to T. The users of this network would be happier if the time to travel from S to T is lower. Intuition tells us that the second configuration where we have an additional link should make the users happier. However, game theoretic analysis proves, using equilibrium analysis, that the first configuration is in fact better for the users.

Fig. 1.1: A transportation network with four nodes

Fig. 1.2: Transportation network with an additional high speed link from A to B

There is considerable evidence for the Braess paradox. For example, in Seoul, South Korea, traffic congestion around the city dramatically reduced when a particular high speed arterial link was closed for traffic as a part of the Cheonggyecheon restoration project. In Stuttgart, Germany, a huge investment was made in decongesting the traffic on the roads by building additional roads but the traffic situation improved only when some of the newly-built roads were closed for traffic. Game theory could be used to obtain scientific predictions of what is likely to happen, by modeling the situation as a game involving the users of the transportation network and capturing their interactions. In chapters 4, 5, and 6, we study this example in some detail.

Vickrey Auction

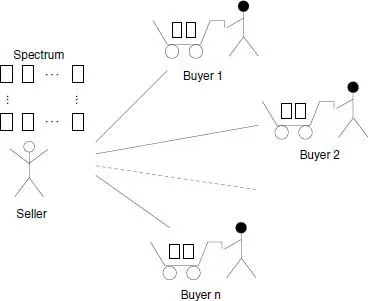
Consider a seller who wishes to allocate an indivisible item to one of n prospective buyers in exchange for a payment. An example would be the sale of a spectrum license by the Government to one of several telecom service providers seeking to buy the license (See Figure 1.3). Each player has a certain valuation for the item on sale. For example, in the spectrum license case, imagine that there are four service providers 1, 2, 3, 4 who value the license at Rs. 400 million, Rs. 500 million, Rs. 700 million, and Rs. 1000 million. In a spectrum auction, the Government invites bids from prospective buyers and allocates the license based on an auction protocol. Two simple and common auction methods are first price sealed bid auction and second price sealed bid auction. In the first price auction, the one who bids highest will be allocated the item and the winning bidder will pay an amount equal to the bid. In the second price auction, the one who bids highest will be allocated the item but the winning bidder will pay an amount equal to the second highest bid.

Fig. 1.3: A spectrum auction

Each auction above can be modeled as a game involving the seller and the buyers. In the first price auction, the bidders will bid amounts which are less than their valuations. In the second price auction, the bidding will be more aggressive since the bidders know that they would be paying less than what they bid in case they win. William Vickrey, in his Nobel prize winning work, proved the remarkable result that the bids in the second price auction will be exactly equal to the respective valuations. In fact, Vickrey showed that it is best for every bidder to bid her true valuation irrespective of whatever is bid by the other players. In the example above, if second price auction is employed, then the players will bid their valuations and the license will be awarded to player 4. This player will pay an amount equal to Rs. 700 million which is the second highest bid. Thus the seller who does not know the valuations of the bidders is able to extract these valuations in the form of their bids. Game theory and mechanism design constitute the science behind the design of a whole gamut of auction protocols which are ubiquitous and extensively used these days.

Divide the Dollar Game

Suppose there are three individuals who wish to divide a total wea...

Table of contents

• Cover
• Halftitle
• front1
• Title
• Copyright Page
• Preface
• Dedication
• Foreword
• Opinions on the Book
• About the Author
• Preface
• Acronyms
• Symbols and Notations
• Contents
• 1. Introduction and Overview
• NON-COOPERATIVE GAME THEORY
• MECHANISM DESIGN
• COOPERATIVE GAME THEORY
• Index