Evolution Equations With A Complex Spatial Variable

Ciprian G Gal, Sorin G Gal, Jerome A Goldstein

• Publisher: WSPC
• Year: 2014
• eBook ISBN: 9789814590617
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

This book investigates several classes of partial differential equations of real time variable and complex spatial variables, including the heat, Laplace, wave, telegraph, Burgers, Black–Merton–Scholes, Schrödinger and Korteweg–de Vries equations.

The complexification of the spatial variable is done by two different methods. The first method is that of complexifying the spatial variable in the corresponding semigroups of operators. In this case, the solutions are studied within the context of the theory of semigroups of linear operators. It is also interesting to observe that these solutions preserve some geometric properties of the boundary function, like the univalence, starlikeness, convexity and spirallikeness. The second method is that of complexifying the spatial variable directly in the corresponding evolution equation from the real case. More precisely, the real spatial variable is replaced by a complex spatial variable in the corresponding evolution equation and then analytic and non-analytic solutions are sought.

For the first time in the book literature, we aim to give a comprehensive study of the most important evolution equations of real time variable and complex spatial variables. In some cases, potential physical interpretations are presented. The generality of the methods used allows the study of evolution equations of spatial variables in general domains of the complex plane.

Contents:

• Historical Background and Motivation
• Heat and Laplace Equations of Complex Spatial Variables
• Higher-Order Heat and Laplace Equations with Complex Spatial Variables
• Wave and Telegraph Equations with Complex Spatial Variables
• Burgers and Black–Merton–Scholes Equations with Complex Spatial Variables
• Schrödinger-Type Equations with Complex Spatial Variables
• Linearized Korteweg–de Vries Equations with Complex Spatial Variables
• Evolution Equations with a Complex Spatial Variable in General Domains

Readership: Graduates and researchers in partial differential equations and in classical analytical function theory of one complex variable.
Key Features:

• For the first time in literature, the study of evolution equations of real time variable and complex spatial variables is made
• The study includes some of the most important classes of partial differential equations: heat, Laplace, wave, telegraph, Burgers, Black–Merton–Scholes, Schrodinger and Korteweg–de Vries equations
• The book is entirely based on the authors' own work

Chapter 1

Historical background and motivation

In this introductory chapter we present the main historical background and motivations supporting the writing of this book.

1.1Historical background on the heat equation

It is generally accepted that by an evolution equation for an unknown function u is understood as any partial differential equation that contains the derivative of u with respect to time. One of the most important and oldest evolution equation is the heat equation, whose Cauchy problem in one-dimension can be stated, for example, as follows:

where f ∈ BUC(ℝ), which is defined as the space of all bounded uniformly continuous functions on ℝ. Here t is the temporal variable and x represents the spatial variable.

The separation of variables solution technique for this equation was proposed by Joseph Fourier in his famous treatise titled Théorie Analytique de la Chaleur, published in 1822. Also, another well-known classical method states that its unique bounded solution is given by the semigroup of linear operators (see, e.g., Goldstein [39]):

The study of the one-dimensional heat equation can be classified after the values taken by its variables t and x, as follows:

Case 1 Both temporal and spatial variables t and x are real (more exactly t is positive and x is real). Here we also include the case when x ∈ ℝⁿ, with n ≥ 2.

Case 2 The temporal variable t is complex and the spatial variable x is real.

Case 3 Both temporal and spatial variables t and x are complex.

Case 4 The temporal variable t is real and the spatial variable x is complex (or hypercomplex).

Case 1 is probably the most studied and appears in many classical papers and books, one of them already mentioned above. For this reason we do not refer to this case here. In Case 2, the theory of analytic semigroups T_t, which can, as functions of the temporal variable t, be continued holomorphically into a sector of the complex plane containing the positive t-axis (see, e.g., Goldstein [39]) is also classical. Since this case was investigated extensively we do not insist on it here. In Case 3, it was first observed by Kovalevskaya [57] that, for the Cauchy problem associated with the heat equation, with time variable τ = t + iη, and spatial variable z = x + iy, both complex,

there are examples of holomorphic non-entire functions F such that the formal power series solution does not converge in any neighborhood of w₀. More exactly, Kovalevskaya [57] gives an example indicating that if F has a finite radius of convergence but is not entire, then the formal series solution of the above problem (1.3) will not converge in any neighborhood of τ₀. Although Kovalevskaya [57] does not actually prove a theorem, by exploiting her ideas in that paper, Khavinson-Shapiro [54] were able to prove several rigorous results concerning the solution of (1.3). In particular, they proved the following two results.

Theorem 1.1.1. If u(τ, z) is holomorphic and it satisfies (1.3) in some neighborhood of (τ₀, z₀), say, in the bi-disk

Δ(τ₀, z₀; r) = {(τ, z) ∈ ℂ²; |τ − τ₀| < r, |z − z₀| < r},

then u can be extended holomorphically to the ”tube”

T (τ₀; r) = {(τ, z...

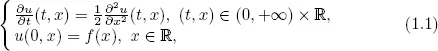
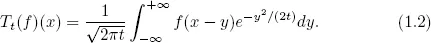
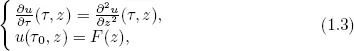
Table of contents

• Cover Page
• Title
• Copyright
• Dedication
• Preface
• Contents
• 1. Historical background and motivation
• 2. Heat and Laplace equations of complex spatial variables
• 3. Higher-order heat and Laplace equations with complex spatial variables
• 4. Wave and telegraph equations with complex spatial variables
• 5. Burgers and Black-Merton-Scholes equations with complex spatial variables
• 6. Schrödinger-type equations with complex spatial variables
• 8. Evolution equations with a complex spatial variable in general domains
• Bibliography
• Index