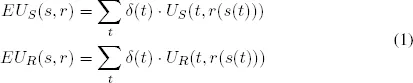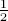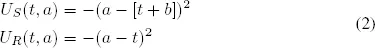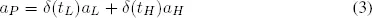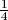Evolution Of Language, The - Proceedings Of The 10th International Conference (Evolang X)

Proceedings of the 10th International Conference

Erica A Cartmill, Seán Roberts, Heidi Lyn, Hannah Cornish

• Publisher: WSPC
• Year: 2014
• eBook ISBN: 9789814603645
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

This volume comprises refereed papers and abstracts of the 10th International Conference on the Evolution of Language (EVOLANGX), held in Vienna on 14–17th April 2014. As the leading international conference in the field, the biennial EVOLANG meeting is characterised by an invigorating, multidisciplinary approach to the origins and evolution of human language, and brings together researchers from many subject areas, including anthropology, archaeology, biology, cognitive science, computer science, genetics, linguistics, neuroscience, palaeontology, primatology and psychology.

For this 10th conference, the proceedings will include a special perspectives section featuring prominent researchers reflecting on the history of the conference and its impact on the field of language evolution since the inaugural EVOLANG conference in 1996.

Contents:

• Diachronic Processes in Language as Signaling Under Conflicting Interests (Christopher Ahern and Robin Clark)
• Syntactic Development in Phenotypic Space (Lluís Barceló-Coblijn and Antoni Gomila Benejam)
• Linguistic Animals: Understanding Language Through a Comparative Approach (Piera Filippi)
• Social Interaction Influences the Evolution of Cognitive Biases for Language (Seán G Roberts, Bill Thompson and Kenny Smith)
• Symbol Extension and Meaning Generation in Cultural Evolution for Displaced Communication (Kaori Tamura and Takashi Hashimoto)
• The Origins of Combinatorial Communication (Richard A Blythe and Thomas C Scott-Phillips)
• Social Origins of Rhythm? Synchrony and Temporal Regularity in Human Vocalization (Daniel L Bowling, Christian T Herbst and W Tecumseh Fitch)
• The Effect of Pitch Enhancement on Spoken Language Acquisition (Piera Filippi, Bruno Gingras and W Tecumseh Fitch)
• Bow-and-Arrow Technology: Mapping Human Cognition and Perhaps Language Evolution (Alexandra Regina Kratschmer, Miriam Noël Haidle and Marlize Lombard)
• The Cognitive Underspinnings of Metaphor as the Driving Force of Language Evolution (Andrew D M Smith and Stefan H Höfler)
• Model Fitting and Prediction for Language Evolution (Bill Thompson and Vanessa Ferdinand)
• and other papers

Readership: Graduate students, academics and researchers working on the evolution of language, artificial intelligence, genetics and psychology.

Papers

DIACHRONIC PROCESSES IN LANGUAGE AS SIGNALING UNDER CONFLICTING INTERESTS

CHRISTOPHER AHERN, ROBIN CLARK

Department of Linguistics, University of Pennsylvania, 619 Williams Hall, Philadelphia, 19104, United States
[email protected], [email protected]

Game-theory has found broad application in modeling pragmatic reasoning in cases of common and conflicting interests. Here we extend these considerations to diachronic patterns of language use. We use evolutionary game theory to characterize the effect of conflicting interests on linguistic signaling in a population over time. We show how sufficiently large conflicts of interest give rise to particular patterns of signaling that can be used to model diachronic processes such as Jespersen’s Cycle.

1. Introduction

In the abstract, both Linguistics and Animal Communication deal with the transmission and interpretation of signals. Yet, the two differ markedly in the use of the term cooperation. Crucially, this difference hinges on the interests of the agents sending and receiving signals. In the Gricean tradition, speakers are taken to be cooperative when they make their contributions relevant to current conversational goals. This use presumes that interlocutors agree to the goals of a given exchange, and benefit from pursuing them. In the biological sense, speakers are cooperative when they forgo some gain to the benefit of others (Nowak, 2006). This use entails that speakers have countervailing goals, but do not pursue them. In what follows, we will use cooperation solely in the biological sense and consider the implications it has for patterns of signaling over time.

Cooperation in the biological sense is in need of evolutionary explanation. If senders have an incentive to pursue some goal, then they should do so. If, in doing so, senders have every incentive to deceive, then receivers should not listen. If receivers do not listen, then senders have no motive to signal in the first place. Crucially, the actions of senders depend on those of receivers and vice versa. Given this interdependence, conflicting interests undermine signaling. Senders will learn or evolve to dissimulate and receivers will learn or evolve to distrust. This process takes on the familiar form of the tragedy of the commons (Hardin, 1968). Individuals will always be tempted to exploit the common resource of credulity, to the collective detriment.

Silence or, at best, meaningless babble is the equilibrium state in the population: neither senders nor receivers have reason to unilaterally change their behavior. So, what keeps signaling in general, and human language in particular, from the downward spiral to silence? The existence and persistence of signaling necessitate evolutionary mechanisms that mitigate conflicts of interest between senders and receivers. Various mechanisms have been proposed to solve this problem, with varying degrees of appropriateness for application to language (Scott-Phillips, 2008).

This leads us to two general questions, which we can consider apart from the details of any particular set of mechanisms. First, how effective are these mechanisms in solving the problem of cooperation in signaling? Given that language exists, such mechanisms are clearly sufficient to stave off total collapse. Given that signals are not always used cooperatively, such mechanism are not sufficient to ensure the idealized case of Gricean commonality. Second, if language is indeed subject to a host of competing pressures, what impact will this have on how linguistic signals are used over time? This second question will be our chief concern.

Using evolutionary game theory, we consider the range of conflict between senders and receivers, from pure common interest to pure conflicts of interest. We identify the crucial points that determine different regimes of signaling behavior: small conflicts allow for stable signaling, large conflicts lead to a collapse, and in between we observe cyclic signaling. The main contribution of this work is the application of this model to the well-known diachronic process of Jespersen’s Cycle. We show how even a slight tendency to overuse emphatic negation leads to the loss of emphasis, necessitating the introduction of a new emphatic form to take its place. This provides a broader connection between the forces affecting language at both evolutionary and historical time scales.

The rest of the paper is organized as follows. In the next section we provide an overview of the formal framework. We then turn to a particular parametrization of conflicting interests and examine stability. The resulting model is then applied to the cycle. We conclude with a brief discussion of our results and directions for future research.

2. Evolutionary Game Theory

Evolutionary game theory (Maynard Smith, 1982) gives us the formal tools to model interactions between agents with varying degrees of common and conflicting interests, without the too strong assumption of perfect rationality. Here we introduce signaling games (Lewis, 1969) along with the equilibrium concept of an evolutionarily stable strategy as a model of signaling in a population.

2.1. Signaling Games

A signaling game consists of two players: a sender and a receiver. The sender has some private piece of information, t ∈ T. The piece of information can be thought of as some fact about the state of the world. The sender chooses a message, m ∈ M, to send to the receiver. A sender strategy s ∈ [T → M] specifies what message to send in any given state.^a The receiver does not know what state of the world actually holds and must choose an action, a ∈ A, to interpret the message sent. A receiver strategy r ∈ [M → A] specifies what action to take upon receiving any message. The outcome of the game is determined by the state of the sender, the message sent, and the action taken by the receiver. The sender and the receiver have preferences over these outcomes, which are reflected in the utility functions, U_S and U_r respectively, which map outcomes to the set of real numbers.

The set of possible combinations of sender and receiver strategies are strategy profiles. That is a sender strategy in the set of possible sender strategies, s ∈ S, and a receiver strategy in the set of all possible receiver strategies, r ∈ R, yield a strategy profile 〈s, r〉. The expected utility for a given strategy profile can be given as follows, where δ specifies a probability distribution over T.

For each possible state the sender and receiver strategies determine an outcome. s(t) is the message the sender will employ and r(s(t)) is the action the receiver will take given that message. The expected utility is the sum of these outcomes weighted by the probability of the state that yields them.

2.2. Evolutionarily Stable Strategies

Signaling games provide a description of the interaction we are interested in, but we require some sort of solution concept to complete our model. An evolutionarily stable strategy (Maynard Smith, 1982) provides just that. Loosely speaking, a strategy is evolutionarily stable if, when played by an entire population, it is resistant to invasion by mutant strategies. For asymmetric games, such as signaling games, where players have different roles, a strategy profile is evolutionarily stable if and only if it constitutes a Strict Nash equilibrium (Selten, 1980).

Definition 1. A strategy profile 〈s*, r*〉 is a Strict Nash equilibrium if and only if:

• For all s ∈ S, such that s ≠ s*, EU_S (s*, r*) > EU_S (s, r*)
• For all r ∈ R, such that r ≠ r*, EU_R (s*, r*) > EU_S (s*, r)

This simply states that the sender and receiver do worse if they unilaterally deviate from the equilibrium. Thus for a given strategy profile to be an ESS its component strategies must be mutual best responses to each other.

3. Conflicting Interests

With the general framework in place, we now turn to a simple way of capturing the degree of conflict between senders and receivers by a single parameter. We then consider different constraints on signaling behavior. From this we determine the existence of evolutionarily stable strategies at various parameter values.

3.1. Parametrization

Conflicts of interest between a sender and the receiver are essentially a matter of misaligned preferences. To see this, consider the following game. Let there be two states T = {t_L, t_H}, where we treat t_L as a low value on some scale and t_H as a high value. For simplicity, t_L = 0 and t_H = 1, where both states are equiprobable, δ(t_L) = δ(t_H) =

. There is some finite set of messages M = {m₁, ..., m_k} available to the sender. Let the set of actions available to the receiver be the interval A = [0,1].

Now, we can consider preferences over outcomes. Receivers want to accurately sort the senders by type and act accordingly. For example, suppose there are actions a_L and a_H that maximize the receiver’s utility when playing with t_L and t_H senders respectively. Following Crawford and Sobel (1982), we define the sender and receiver utility functions as the following, where the constant of conflict, b ∈ [0,1], allows us to express how much some senders gain by exaggeration.

Note that the constant of conflict represents the distance between the interests of the sender and the receiver. When b = 0 interests are perfectly aligned. Senders wish to reveal their type: a t_L sender’s payoff is maximized by a_L and a t_H sender’s payoff is maximized by a_H. These actions also maximize the receiver’s payoff. In contrast, when b > 0, their interests diverge. The sender does best when he convinces the receiver to take an action appropriate for a higher type. For example, if b = 1 then senders maximize their utility with the highest possible action. A t_L sender’s payoff is maximized by a_H, as is a t_H sender’s payoff. Note that a t_H sender’s payoff is always maximized by a_H, regardless of the size b.

3.2. Signaling

We can now consider the incentives of senders and receivers and define conditions that determine signaling behavior. We begin from the receiver’s perspective before turning to the sender.

The receiver’s best course of action depends on the amount of information available regarding the sender’s type. For example, if senders separate themselves by using distinct signals, then the receiver should make use of this information by taking the unique appropriate action. What should the receiver do if the senders pool together using the same signal? In the absence of any information, the action that maximizes her expected utility is the action that corresponds to the average type of the population, which we will refer to as the pooling action, a_P.

We can now turn to the sender’s perspective and ask which of the receiver’s actions are preferred. We can state this generally in the following manner. For a sender of type t, the expected utility of an action a′ exceeds that of an action a, where a′ > a, if the following holds.

In other words, when the sender’s type plus the constant of conflict exceed the average of the two actions, then the higher action a′ is preferred. This gives us a general recipe for determining the sender’s preferences. For any two receiver actions we can find their average. If this is less than the sender’s type plus the conflict, then the sender prefers the alternative higher action.

3.3. Stability

We are now in a position to consider the stability of various sorts of signaling behavior for various degrees of conflict. In particular, we will be interested in whether senders separate or pool, and any transitions between the two kinds of behavior. As a point of reference, we will consider a state of affairs where all sender types use a single message m, and receivers respond to this message with the pooling action a_P. Now, consider the availability of some alternate message m′, a neologism. Suppose that receivers take some action other than a_P in response to this message. When would senders have an incentive to adopt a new message? The answer to this question depends on the degree of conflict.

Consider the case where b is fairly small. Starting from the pooling state, do senders prefer some alternate action? We consider the types in turn. For b ∈ [0,

), t_L senders prefer a_L to a_P and t_H sen...

Table of contents

• Cover Page
• Title Page
• Copyright
• Preface
• Program Committee
• Contents
• Perspectives on EVOLANG
• Papers
• Abstracts
• Authors Index