Problems in Probability

T M Mills

• Publisher: WSPC
• Year: 2013
• eBook ISBN: 9789814551472
• Edition: 2
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

This is a book of problems in probability and their solutions. The work has been written for undergraduate students who have a background in calculus and wish to study probability.

Probability theory is a key part of contemporary mathematics. The subject plays a key role in the insurance industry, modelling financial markets, and statistics in general — including all those fields of endeavour to which statistics is applied (e.g. health, physical sciences, engineering, economics, social sciences). Every student majoring in mathematics at university ought to take a course on probability or mathematical statistics. Probability is now a standard part of high school mathematics, and teachers ought to be well versed and confident in the subject. Problem solving is important in mathematics. This book combines problem solving and probability.

Contents:

• Sets, Measure and Probability
• Elementary Probability
• Discrete Random Variables
• Continuous Random Variables
• Limit Theorems
• Random Walks

Readership: Undergraduates and lecturers in probability.

PART 1

Problems

Chapter 1

Sets, measure and probability

1.1 Notes

Logic

If p, q denote propostions then

¬p denotes the proposition “not p”;

p ∧ q denotes the proposition “p and q”;

p ∨ q denotes the proposition “p or q”;

p ⇒ q denotes the proposition “p implies q”;

p ⇔ q denotes the proposition “p implies q and q implies p”;

(∀x)(p) denotes the proposition “for all x, p is true”;

(∃x)(p) denotes the proposition “there exists an x such that p is true”.

Sets

x ∈ A: x belongs to the set A; x is an element of the set A

x ∉ A: x is not an element of the set A

A ⊂ B: A is a subset of B; x ∈ A ⇒ x ∈ B

A = B: A ⊂ B and B ⊂ A; x ∈ A ⇔ x ∈ B

A ∪ B = {x : x ∈ A or x ∈ B}

A ∩ B = {x : x ∈ A and x ∈ B}

A′ = {x : x ∉ A}

A \ B = A ∩ B′

A ∆ B = (A ∩ B′) ∪ (B ∩ A′)

Commutative laws:

(A ∩ B) = (B ∩ A)

(A ∪ B) = (B ∪ A)

Associative laws :

(A ∩ B) ∩ C = A ∩ (B ∩ C) = A ∩ B ∩ C

(A ∪ B) ∪ C = A ∪ (B ∪ C) = A ∪ B ∪ C

Distributive laws :

(A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C)

(A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C)

Complementation laws:

(A ∩ A′) =

(A ∪ A′) = Ω (where Ω denotes some universal set)

De Morgan’s laws :

(A ∩ B)′ = (A′ ∪ B′)

(A ∪ B)′ = (A′ ∩ B′)

Measure and probability

We begin with the definition of a σ-algebra of sets.

Definition 1.1 Let Ω be a set and

be a set of subsets of Ω. Then

is a σ-algebra if

We now define a probability measure.

Definition 1.2 Let Ω be a set and

be a σ-algebra of subsets of Ω. The function P :

→ [0,1] is a probability measure if

Finally we define a probability space.

Definition 1.3 Let Ω be a set,

be a σ-algebra of subsets of Ω and P :

→ [0,1] be a probability measure. Then we say that

• (Ω,

, P) is a probability space,

• the set Ω is called the sample space, and,

• elements of

are called events.

The next definition sets the stage for exploring relations between events.

Definition 1.4 Let (Ω,

, P) be a probability space, and let A and B be events. We say that A and B are independent events if

P(A ∩ B)= P(A)P(B).

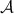
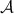
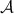
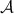
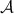
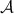
1.2 Problems

(1) Suppose that A, B, C are 3 distinct subsets of Ω. We can construct other distinct subsets of Ω from these 3 subsets using the only the operations ∩ and ∪ repeatedly: A, B, C, A ∩ B, (A ∩ B) ∪ C etc. We say that 2 subsets are different if they are not necessarily equal to each other. For example, A ∩ B is different from A ∩ C, but (A ∩ B) ∪ C is not different from (A ∪ C) ∩ (B ∪ C).
According to Rényi [54, p.26] there are 18 different subsets that can be constructed in this way having started with n = 3 distinct subsets A, B, C. Indeed,

• if n = 2, we could create 4 different subsets;

• if n = 3, we could create 18 different subsets;

• if n = 4, we could...

Table of contents

• Cover
• HalfTitle
• FrontMatter
• TitlePage
• Copyright
• Dedication
• Preface
• Contents
• Part 1 Problems
• Part 2 Solutions
• Bibliography
• Index