Spanning Tree Results For Graphs And Multigraphs: A Matrix-theoretic Approach

A Matrix-Theoretic Approach

Daniel J Gross, John T Saccoman, Charles L Suffel

• Publisher: WSPC
• Year: 2014
• eBook ISBN: 9789814566056
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

This book is concerned with the optimization problem of maximizing the number of spanning trees of a multigraph. Since a spanning tree is a minimally connected subgraph, graphs and multigraphs having more of these are, in some sense, immune to disconnection by edge failure. We employ a matrix-theoretic approach to the calculation of the number of spanning trees.

The authors envision this as a research aid that is of particular interest to graduate students or advanced undergraduate students and researchers in the area of network reliability theory. This would encompass graph theorists of all stripes, including mathematicians, computer scientists, electrical and computer engineers, and operations researchers.

Contents:

• An Introduction to Relevant Graph Theory and Matrix Theory
• Calculating the Number of Spanning Trees: The Algebraic Approach
• Multigraphs with the Maximum Number of Spanning Trees: An Analytic Approach
• Threshold Graphs
• Approaches to the Multigraph Problem
• Laplacian Integral Graphs and Multigraphs

Readership: Graduate students and researchers in combinatorics and graph theory. Key Features:

• Unlike this book, very few books cover a significant amount of material about the Laplacian matrix, nor do they contain an extensive treatment of counting or optimizing the number of spanning trees
• Other works in the field do not devote to multigraphs

Chapter 1

Calculating the Number of Spanning Trees: The Algebraic Approach

In this chapter, we explore the algebraic method of computing t(M), the number of spanning trees of a multigraph M. We then apply these techniques to some special families of graphs.

A formal probabilistic reliability model, All Terminal Reliability (ATR), can be described as follows: the edges of a multigraph M are assumed to have equal and independent probabilities of operation p, and the reliability R(M, p) of a multigraph is defined to be the probability that a spanning connected subgraph operates. If

denotes the number of spanning connected subgraphs having i edges, then it is easily verified that

For small values of p, the polynomial will be dominated by the

term, and since

is the number of spanning trees, graphs with a larger number of spanning trees will have greater reliability for such p.

In graph theory, most of the results regarding the number of spanning trees have only been proven for graphs, so in addition to an exposition of results for graphs, we will investigate the problem for the extended class of multigraphs. It should be noted that, while extensions to multigraphs make the optimal solution readily apparent in many problems, this is not the case for the spanning tree problem.

1.1 The Node-Arc Incidence Matrix

Consider a directed multigraph

with n nodes, {v₁,v₂,…, v_n}, and e arcs,

. We define an n×e matrix, called the node-arc incidence matrix

, which uniquely characterizes

by

Example 1.1 The directed multigraph depicted in Figure 1.1 has node-arc incidence matrix

Figure 1.1: A directed multigraph.

Since each arc has exactly two end-nodes, the sum of the row vectors of S is

. Clearly, any single row can be deleted from S without losing any information about

. The matrix resulting from the deletion of the i^th row is called a reduced node-arc incidence matrix, and is denoted

, i.e., in terms of the notation ...

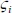
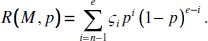
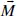
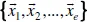
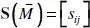
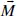
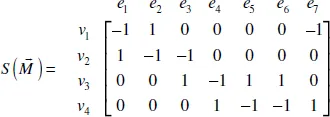
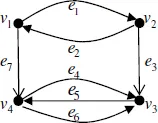
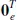
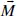
Table of contents

• Cover page
• Halftitle page
• Title page
• Copyright page
• Dedication page
• Preface
• Contents
• 0   An Introduction to Relevant Graph Theory and Matrix Theory
• 1   Calculating the Number of Spanning Trees: The Algebraic Approach
• 2   Multigraphs with the Maximum Number of Spanning Trees: An Analytic Approach
• 3   Threshold Graphs
• 4   Approaches to the Multigraph Problem
• 5   Laplacian Integral Graphs and Multigraphs
• Bibliography
• Index