A Participatory Approach to Modern Geometry

Jay Kappraff

• Publisher: WSPC
• Year: 2014
• eBook ISBN: 9789814556729
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

This book aims to make the subject of geometry and its applications easy and comfortable to understand by students majoring in mathematics or the liberal arts, architecture and design. It can be used to teach students at different levels of computational ability and there is also sufficient novel material to interest students at a higher cognitive level. While the book goes deeply into the applications of geometry, it contains much introductory material which up to now may not have been known to the student. The constructive approach using compass and straightedge engages students, not just on an intellectual level, but also at a tactile level. This may be the only rigorous book offering geometry that attempts to engage students outside of the mathematics discipline. Contents:

• Triangle and Square Grids
• The Pythagorean Theorem
• Scan Converting of a Line Segment
• Compass and Straightedge Constructions (Part 1: The World Within a Triangle)
• Congruent Triangles
• Introduction to Trigonometry
• The Art of Proof
• Angle
• Voronoi Domains
• Parallel Lines
• Bracing a Framework
• Similarity
• Compass and Straightedge Constructions (Part 2: Doing Algebra with Geometry)
• Area
• Vectors and Geoboards
• Logarithmic Spirals
• The Golden and Silver Means
• Isometries
• Isometries and Mirrors
• Kaleidoscopes and Symmetry
• Groups and Kaleidoscope Symmetry
• Frieze Patterns
• An Introduction to Fractals
• Isometries and Matrices

Readership: Undergraduate students of any discipline interested in improving their visual understanding in geometry. Key Features:

• Engages the student in hands-on activities using compass, straightedge, and protractor. In talking about areas and vectors, geoboards are used. A giant fractal wallhanging is constructed using the iterative function system. Compass and straightedge is used to create wonderful patterns
• There are many novel topics not covered in other books on geometry such as logarithmic spirals, Voronoi domains with application to pattern recognition, parallel lines with application to bracing a framework, fractals, kaleidocopes, an introduction to group theory
• Projective geometry is introduced at a constructive level. The student is engaged in carrying out 13 fundamental constructions of projective geometry. By focusing on projective geometry, the properties of Euclidean geometry become more understandable — including the nature of infinity and the meaning of parallel lines

	CHAPTER 1
TRIANGLE AND SQUARE GRIDS

1.1.Introduction

The power and potential that exists by the simple act of drawing a circle or a square is amazing. This was recognized in ancient times where the circle symbolized the celestial sphere and represented the Heavenly domain; the square, with its reference to the four directions of the compass, represented the Earthly domain. Margit Echols [Ech] was a quilter who used geometry as the basis of her wonderful quilt patterns. In this chapter, Echols shows how to create triangle and square grids beginning with a circle. The grids then become scaffolding for the creation of a limitless number of repeating patterns. These patterns are sometimes referred to by sacred geometers as The Flower of Life [Flo], [Kap2].

1.2.Triangle-Circle and Triangle Grids

For this exercise, you may use either a compass or a software program such as Corel Draw, Adobe Illustrator, or Geometer’s Sketchpad to create circles. To create a triangle grid, start with a circle. Place the compass point on the circumference and draw another circle with the same radius. The resulting pair of circles is perhaps the most fundamental structure in geometry called the Vesica Pisces shown in Fig. 1.1a. This figure had sacred significance in the Christian religion. It is found in many churches where images of Christ were drawn in the central fish-like region as shown in Fig. 1.1b. The Vesica Pisces is created by starting with a line and a single point on the line which is the center of a circle as shown in Fig. 1.2. Where the line intersects the circle, draw another circle of the same radius. The Vesica Pisces is the starting point of a triangle-circle grid. Figure 1.3 shows how to generate such a grid step by step. By Step 9, you have created a triangle grid. Look within the grid. Can you see a grid of hexagons embedded in the grid of equilateral triangles? Islamic artists designed patterns with hexagons and 6-pointed stars on this grid from the center outward with no gaps and no overlaps as seen in the shaded stars of the triangular grid in Fig. 1.4.

Fig. 1.1. (a) The Vesica Pisces; (b) marble relief of Christ in a Vesica.

Fig. 1.2. Geometry begins with a point, a line and a circle.

Pattern Puzzle A is presented in Fig. 1.5a. These patterns are hidden in the triangle-circle system of Fig. 1.5b. Draw each of these patterns using the overlapping circles in Fig. 1.6b as a guide. You can add color. Note that some patterns can be traced directly from the curved lines, while the triangle grid can be drawn using a straightedge to connect points where the circles intersect. Many other patterns can be found in this triangle, such as the circle grid. Try to find others, or invent some of your own. The possibilities are endless!

Fig. 1.3. Nine steps to drawing a triangle-circle grid.

Pattern Puzzle B is presented in Fig. 1.6a. Look for these patterns hidden in the triangle grid in Fig. 1.6b. You can either shade or add color. You can also draw each one on a sheet of tracing paper using the underlying grid as a guide or use your computer drawing programs. You may try creating patterns of your own. Again, there are an infinite number of possibilities.

Fig. 1.4. Islamic artists designed star and hexagonal patterns on a triangular grid.

Fig. 1.5. (a) Pattern puzzle A. Can you find these patterns in the triangle-circle grid?; (b) A triangle-circle grid.

Fig. 1.6. (a) Pattern puzzle B. Can you find these patterns in the triangle grid?; (b) A triangle grid.

1.3.Square-Circle and Square Grids

Whereas the triangle-circle grids were created by beginning with a line and a single point on it, square-circle patterns begin with a pair of lines intersecting at a right angle. The point of intersection of these lines defines the center of a circle. A circle is drawn about this center in order to define the four points where the pair of perpendicular lines intersect the circle. The initial circle is then removed. The four new points are centers of new circles with the same radius. The points where two circles intersect define the centers of new circles of the square-circle grid. Construct a square-circle grid by following the procedure in Fig. 1.7 step by step. This grid again leads to countless designs, ten of which are shown in Pattern Puzzle C in Fig. 1.8.

Fig. 1.7. Nine steps to drawing a circle and square grid and the star-cross pattern.

1.4.Star Designs Based on the Triangle Grid

Beginning with the triangle-circle grid as shown in Fig. 1.9, six- and twelve-pointed stars can be constructed. For this exercise you can also use a coffee can cover instead of a compass to carry out the construction in which the center of the cover has the usual marking; you simply place the center of the coffee can cover over the point that you would otherwise place your compass point to draw the circle. Beginning with the square-circle grid, eight- and sixteen-pointed stars can be created as shown in Fig. 1.10.

Fig. 1.8. Pattern puzzle C. Can you find these patterns in the square-circle grid?

Fig. 1.9. Drawing 6- and 12-pointed stars.

Construction 1: Use Adobe Illustrator, Corel Draw or simply a compass and straightedge to create a triangle-circle grid and a triangle grid beginning with a circle. After doing this, create your own pattern based on the triangle-circle grid and the triangle grid.

Fig. 1.10. Drawing 8- and 16-pointed stars.

Construction 2: Beginning with a circle, repeat the instructions for Construction 1 to construct a pattern of your own based on the square-circle and square grids.

Construction 3: Repeat the instructions for Construction 1 and create star patterns based on six-, eight-, twelve- and sixteen-pointed stars. Alternatively you can experiment with other stars of your choice. Be bold and try to create an ...

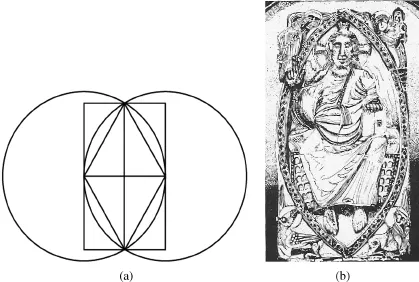
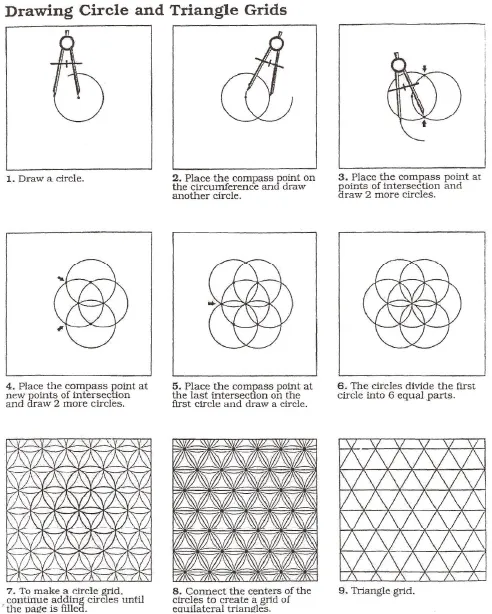
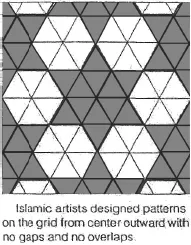
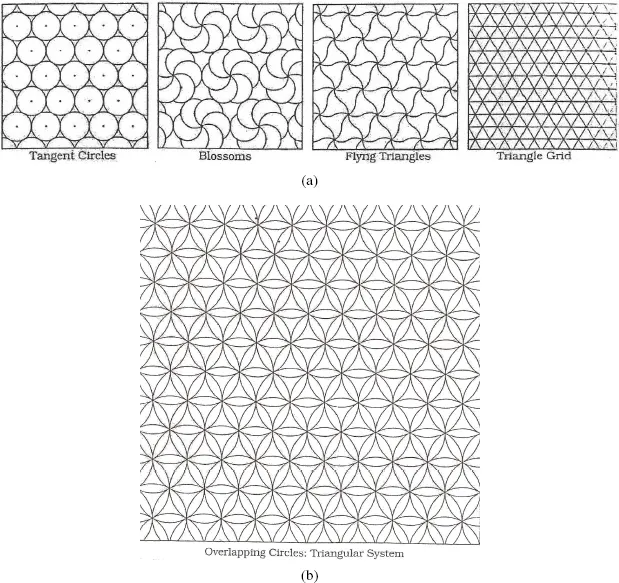
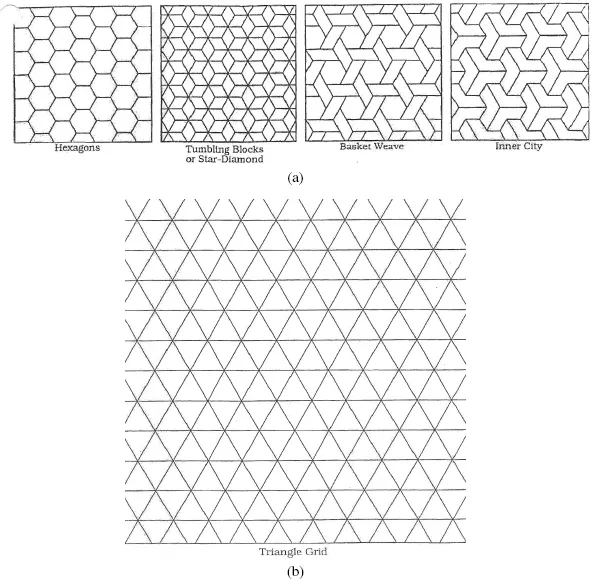
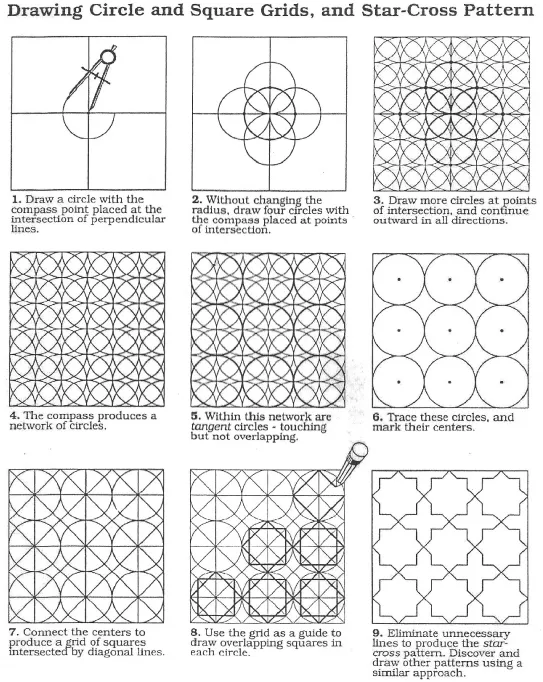
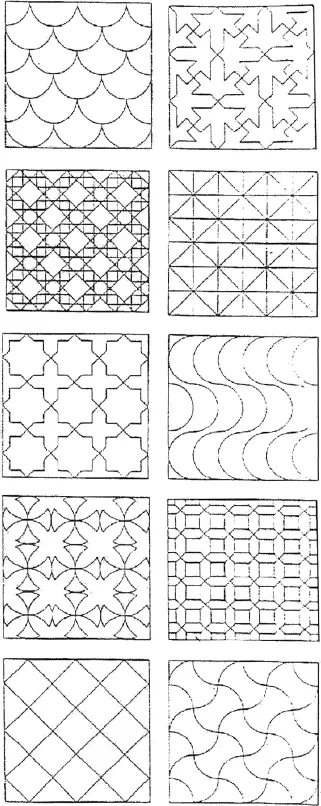
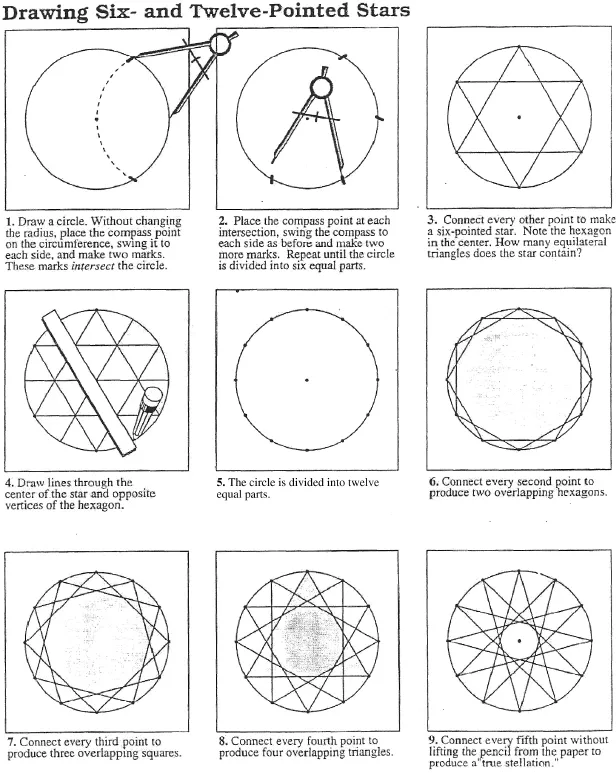
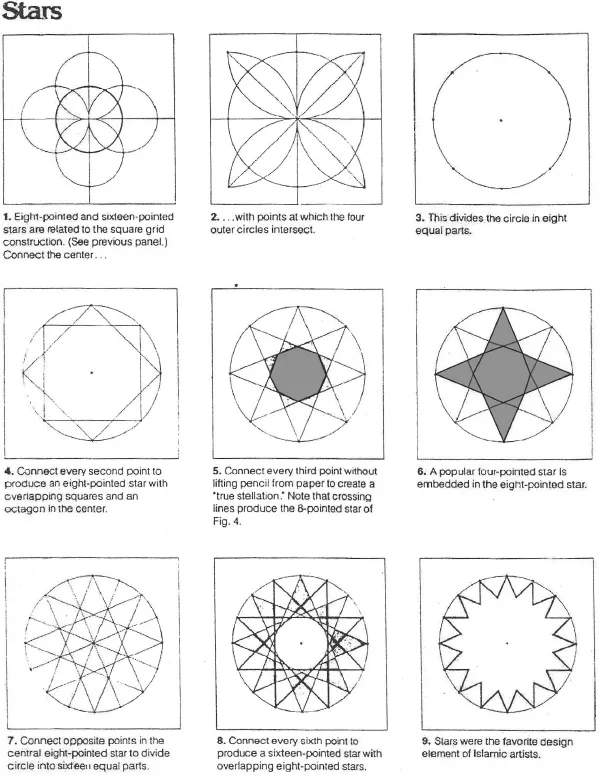
Table of contents

• Cover Page
• Title Page
• Copyright Page
• Contents
• Preface
• Chapter 1. Triangle and Square Grids
• Chapter 2. The Pythagorean Theorem
• Chapter 3. Scan Converting of a Line Segment
• Chapter 4. Compass and Straightedge Constructions
• Chapter 5. Congruent Triangles
• Chapter 6. Introduction to Trigonometry
• Chapter 7. The Art of Proof
• Chapter 8. Angle
• Chapter 9. Voronoi Domains
• Chapter 10. Parallel Lines
• Chapter 11. Bracing a Framework
• Chapter 12. Similarity
• Chapter 13. Compass and Straightedge Constructions
• 14. Area
• 15. Vectors and Geoboards
• 16. Logarithmic Spirals
• 17. The Golden and Silver Means
• 18. Isometries
• 19. Isometries and Mirrors
• 20. Kaleidoscopes and Symmetry
• 21. Groups and Kaleidoscope Symmetry
• 22. Frieze Patterns
• 23. An Introduction to Fractals
• 24. Isometries and Matrices
• Appendix A: Projective Geometry Constructions
• Appendix B: Glossary
• Appendix C: Essays
• Bibliography
• Index