Lie Groups And Lie Algebras For Physicists

Ashok Das, Susumu Okubo

• Publisher: WSPC
• Year: 2014
• eBook ISBN: 9789814603294
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

The book is intended for graduate students of theoretical physics (with a background in quantum mechanics) as well as researchers interested in applications of Lie group theory and Lie algebras in physics. The emphasis is on the inter-relations of representation theories of Lie groups and the corresponding Lie algebras.
Contents:

• Introduction to Groups
• Representation of Groups
• Lie Algebras
• Relationship between Lie Algebras and Lie Groups
• Irreducible Tensor Representations and Young Tableau
• Clifford Algebra
• Lorentz Group and the Dirac Equation
• Yang–Mills Gauge Theory
• Quark Model and SU F (3) Symmetry
• Casimir Invariants and Adjoint Operators
• Root System of Lie Algebras
• Graduate students, researchers and anyone else with a background in quantum mechanics. Key Features:
  • Many worked examples are included to explain the essential abstract ideas, with derivations of various results given in detail
  • Many new features can be also found including a simple introduction to Cartan–Dynkin theory higher order Casimir invariants as well as exceptional groups

CHAPTER 1

Introduction to groups

In this chapter, we introduce the concept of a group and present in some detail various examples of commonly used groups in physics. This is helpful in establishing the terminology as well as the notations commonly used in the study of groups which will also be useful in further development of various ideas associated with groups.

1.1 Definition of a group

Let us start with the formal definition of a group G as follows:

(G1): For any two elements a and b in a group, a product is defined in G satisfying

(G2): The group product is associative so that

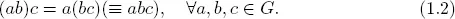
(G3): The group has a unique identity (unit) element e ∈ G such that

This implies that

(G4): Any element a ∈ G has a unique inverse element a⁻¹ ∈ G so that

Any set of elements G satisfying all the axioms (G1)-(G4) is defined to be a group. On the other hand, a set of elements which satisfies only the first three axioms (G1)-(G3), but not (G4), is known as a semi-group. (More rigorously, a semi-group is defined as the set of elements which satisfy only (G1)-(G2). However, one can always add the identity element to the group since its presence, when an inverse is not defined, is inconsequential (see (1.3)-(1.4)) and we will adopt this definition commonly used in physics.)

Some comments are in order here. We note that the definition of a group does not require that the product rule satisfy the commutativity law ab = ba. However, if for any two arbitrary elements of the group, a, b ∈ G, the product satisfies ab = ba, then the group G is called a commutative group or an Abelian group (named after the Norwegian mathematician Niels Henrik Abel). On the other hand, if the product rule for a group G does not satisfy commutativity law in general, namely, if ab = ba for some of the elements a, b ∈ G, then the group G is known as a non-commutative group or a non-Abelian group. Furthermore, it is easy to see from the definition (G4) of the inverse of an element that the inverse of a product of two elements satisfies

in general, unless, of course, the group G is Abelian. Equation (1.6) is easily checked in the following way

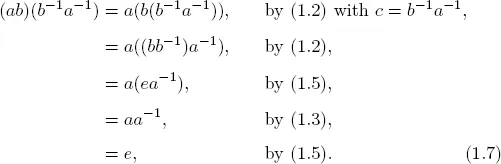
Similarly, it is straightforward to verify that (b⁻¹a⁻¹)(ab) = e.

In order to illustrate the proper definitions in a simple manner, let us consider the following practical example from our day to day life. Let “a” and “b” denote respectively the operations of putting on a coat and a shirt. In this case, the (combined) operation “ab” would correspond to putting on a shirt first (b) and then putting on a coat (a) whereas the (combined) operation “ba” would denote putting on a coat first and then a shirt. Clearly, the operations are not commutative, namely, ab ≠ ba. If we now introduce a third operation “c” as corresponding to putting on an overcoat, then the law of associativity of the operations (1.2) follows, namely, (ca)b = c(ab) = cab and corresponds to putting on a shirt, a coat and an overcoat in that order. It now follows that the operation “bb” denotes putting on two shirts while “b(bb) = (bb)b = bbb” stands for putting on three shirts etc. The set of these operations would define a semi-group if we introduce the identity (unit) element e (see (1.3)) to correspond to the operation of doing nothing. However, this does not make the set of operations a group for the following reason. We note that we can naturally define the inverses “a⁻¹” and “b⁻¹” to correspond respectively to the operati...

Table of contents

• Cover Page
• Title Page
• Copyright
• Preface
• Contents
• 1 Introduction to groups
• 2 Representation of groups
• 3 Lie algebras
• 4 Relationship between Lie algebras and Lie groups
• 5 Irreducible tensor representations and Young tableau
• 6 Clifford algebra
• 7 Lorentz group and the Dirac equation
• 8 Yang-Mills gauge theory
• 9 Quark model and SUF(3) symmetry
• 10 Casimir invariants and adjoint operators
• 11 Root system of Lie algebras
• Index