Exponential Function Approach To Parabolic Equations, An

Chin-Yuan Lin

• Publisher: WSPC
• Year: 2014
• eBook ISBN: 9789814616409
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

This volume is on initial-boundary value problems for parabolic partial differential equations of second order. It rewrites the problems as abstract Cauchy problems or evolution equations, and then solves them by the technique of elementary difference equations. Because of this, the volume assumes less background and provides an easy approach for readers to understand.

Contents:

• Existence Theorems for Cauchy Problems
• Existence Theorems for Evolution Equations (I)
• Linear Autonomous Parabolic Equations
• Nonlinear Autonomous Parabolic Equations
• Linear Non-autonomous Parabolic Equations
• Nonlinear Non-autonomous Parabolic Equations (I)
• The Associated Elliptic Equations
• Existence Theorems for Evolution Equations (II)
• Nonlinear Non-autonomous Parabolic Equations (II)
• Appendix

Readership: Mathematical graduate students and researchers in the area of Analysis and Differential Equations. It is also good for engineering graduate students and researchers who are interested in parabolic partial differential equations.
Key Features:

• The book assumes less background, provides an easy approach, and establishes good results
• It contains recent materials that are interesting to graduate students and researchers

CHAPTER 1

Existence Theorems for Cauchy Problems

1. Introduction

In this chapter, linear and nonlinear Cauchy problems, together with their associated nonhomogeneous problems, will be studied. Those problems will be solved with the aid of elementary difference equations. The obtained results will be illustrated by solving simple, initial-boundary value problems for parabolic, partial differential equations with time-independent coefficients. Further illustrations of solving more general, parabolic partial differential equations with time-independent coefficients will be given in Chapters 3 and 4.

Let constants ω ∈ ℝ and M ≥ 1. Consider the linear Cauchy problem

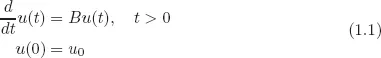
in a real Banach space (X, || · ||), where u is a function from [0, ∞) to X, and

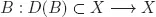
is an unbounded linear operator. Here recall

• A real Banach space is a complete, real normed vector space equipped with a norm.
  For example, the real vector space ℝ of real numbers over the field of itself, equipped with the norm of the usual function | · | of absolute value, is a real Banach space.
  Another example is the real Banach space (C[0, 1], || · ||_∞) of all continuous, real-valued functions on [0, 1], equipped with supremum norm || · ||_∞, where
  
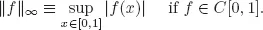
• One example of an unbounded linear operator is the first order ordinary differential operator S in the real Banch space (C[0, 1], || · ||_∞), where
  
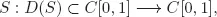  defined by

  

  for f in D(S), the set of all real, continuously differentiable functions on [0, 1].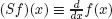

To solve the linear Cauchy problem (1.1), let the simple case be considered first where X = ℝ, and B = b, a real number. In this case, the unique solution is given by

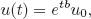
where the exponential function e^tb ...

Table of contents

• Cover Page
• Title Page
• Copyright Page
• Contents
• Preface
• Chapter 1. Existence Theorems for Cauchy Problems
• Chapter 2. Existence Theorems for Evolution Equations (I)
• Chapter 3. Linear Autonomous Parabolic Equations
• Chapter 4. Nonlinear Autonomous Parabolic Equations
• Chapter 5. Linear Non-autonomous Parabolic Equations
• Chapter 6. Nonlinear Non-autonomous Parabolic Equations (I)
• Chapter 7. The Associated Elliptic Equations
• Chapter 8. Existence Theorems for Evolution Equations (II)
• Chapter 9. Nonlinear Non-autonomous Parabolic Equations (II)
• Appendix
• Bibliography
• Index