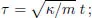Introduction to Modern Physics

Solutions to Problems

Paolo Amore, John Dirk Walecka

• Publisher: WSPC
• Year: 2013
• eBook ISBN: 9789814520331
• Topic: Education
• Subtopic: Teaching Science & Technology

Our understanding of the physical world was revolutionized in the twentieth century — the era of “modern physics”. The book Introduction to Modern Physics: Theoretical Foundations, aimed at the very best students, presents the foundations and frontiers of today's physics. Typically, students have to wade through several courses to see many of these topics. The goal is to give them some idea of where they are going, and how things fit together, as they go along.

The book focuses on the following topics: quantum mechanics; applications in atomic, nuclear, particle, and condensed-matter physics; special relativity; relativistic quantum mechanics, including the Dirac equation and Feynman diagrams; quantum fields; and general relativity. The aim is to cover these topics in sufficient depth that things “make sense” to students, and they achieve an elementary working knowledge of them. The book assumes a one-year, calculus-based freshman physics course, along with a one-year course in calculus. Several appendices bring the reader up to speed on any additional required mathematics. Many problems are included, a great number of which take dedicated readers just as far as they want to go in modern physics.

The present book provides solutions to the over 175 problems in Introduction to Modern Physics: Theoretical Foundations in what we believe to be a clear and concise fashion.

Contents:

• Introduction
• Classical Physics
• Some Contradictions
• Quantum Mechanics
• Atomic Physics
• Nuclear Physics
• Particle Physics
• Special Relativity
• Relativistic Quantum Mechanics
• General Relativity
• Quantum Fluids
• Quantum Fields
• Appendices:
  • Mathematica Program for Problem 2.5
  • Matrices
  • Fourier Series and Fourier Integrals
  • Some Thermodynamics
  • Some Statistical Mechanics
  • Some Vector Calculus
  • Black Body Flux
  • Wave Functions for Identical Particles
  • Transition Rate
  • Neutrino Mixing
  • Units

Readership: Upper-level undergraduate physics or science students, research scientists and engineers.
Key Features:

• Provides solutions to the over 175 problems in the book Introduction to Modern Physics: Theoretical Foundations
• Problems enhance and extend the coverage in that text
• Solutions are presented in a clear and concise fashion
• Provides a learning aid for students
• Provides a teaching aid for instructors

Chapter 1

Introduction

The book Introduction to Modern Physics: Theoretical Foundations starts with the following two paragraphs [Walecka (2008)]:

“At the end of the 19th century, one could take pride in the fact that the laws of physics were now understood. With newtonian mechanics, the statistical analysis of Boltzmann, and Maxwell’s equations for electromagnetism, one had an excellent description of the world we see around us. At that point, a series of experiments were performed whose results simply could not be understood within this classical framework. These experiments probed a microscopic, or high-velocity, world that went far beyond our everyday perception. The resolution of these paradoxes led to the theories of quantum mechanics and special relativity, which provide the foundation of modern physics. Atomic, nuclear, particle, and condensed-matter physics are all built on this foundation. Einstein’s extension of his theory of special relativity to general relativity provides the current basis for our understanding of gravitation and cosmology—physics to the farthest reaches of the universe. The theories of quantum mechanics, special relativity, and general relativity have been remarkably successful. All current experiments can be understood within this framework. The goal of this book is to introduce a reader, with an assumed knowledge of classical physics, to modern physics.¹

It is assumed that the reader has had a good one-year, calculus-based freshman physics course, along with a good one-year course in calculus. A sufficient number of appendices are included to bring the reader up to speed on any additional mathematics required at the outset. Over 175 problems are included in the book, some for each chapter. While there are many problems that directly amplify the material in the text, there are also a great number of them that will take dedicated readers just as far as they want to go in modern physics. Although the book is designed so that one can, in principle, read and follow the text without doing any of the problems, the reader is strongly urged to attempt as many of them as possible in order to obtain some confidence in his or her understanding of the basics of modern physics. With very few exceptions, the reader should find that the text, appendices, and problems form a self-contained volume.”²

As stated in the preface, the publisher has requested that we prepare a solutions manual for the problems in this book. Although the steps required in solving the problems are clearly laid out in the text, it is advantageous to have prepared solutions available. This is useful for instructors as well as students, both to calibrate their own solutions and to see how someone else would go about solving the problems. We write the present book in response to the publisher’s request. Solutions are presented here for all of the problems in the modern physics book. The problems are first restated, and then the solutions given. We try, as far as possible, to follow the notation in the text.

Chapter 2 is on classical physics. Here, motivated by Newton’s laws, there are problems on numerical methods and numerical integration, much facilitated by the mathematics programs now available for personal computers. The motion of a string provides the paradigm for the discussion of continuum mechanics, wave motion, and quantum field theory in the book, and there are several problems on string motion. This also leads directly to the study of Fourier series and Fourier integrals, for which appendices provide a foundation.³ There are problems in classical statistics, and on the basic concepts in classical electricity and magnetism, both again supported in the appendices.

Chapter 3 is concerned with some contradictions with classical physics. Here problems expand on the classical paradoxes encountered in the specific heat of solids, black-body radiation, the Compton effect, and the discrete lines in atomic spectra, paradoxes that led to the Planck hypothesis for the spectral distribution and the Bohr theory of the atom.

Chapter 4 on quantum mechanics contains a large number of supporting problems. The study of wave motion and Fourier integrals provides a base for the development of the Schrödinger equation. The continuity equation, and appropriate boundary conditions, are examined. Exercises are given on partial integration and hermitian operators, and on commutation relations. Ehrenfest’s theorem, which exhibits the proper classical limit, is derived. The rigorous statement of the uncertainty principle is derived and investigated in the motion of the minimal packet. Barrier penetration is examined, and the Schrödinger equation is also solved for both the one-and three-dimensional boxes, and the wave functions studied, as are those for the one-dimensional oscillator and the 1/r potential. The elements of angular momentum are developed. The creation and destruction operators for the oscillator are introduced. Finally there are problems on the low-temperature behavior of non-interacting Bose and Fermi gases.

Chapter 5 in on atomic physics. The spin-orbit interaction is examined, and the Landé g-factor is derived. There are several problems on the Thomas-Fermi model of the atom, where readily available mathematics programs allow one to numerically integrate the non-linear Thomas-Fermi equation. This model provides great insight into the many-body structure of the atom. There are also problems on determining the electronic configuration of atoms and on deducing the implications of that configuration.

Chapter 6 is concerned with nuclear physics. Here the two-body problem is examined, and solved for simple potentials. There are problems on nuclear stability, and the use and applications of the atomic mass tables. There are exercises on the use of the semi-empirical mass formula, and simple derivations of both the Coulomb and symmetry-energy terms appearing in it. The nuclear form factor is calculated. Predictions of the shell model are investigated, and the Schmidt lines for nuclear magnetic moments derived and applied.

Chapter 7 is on particle physics. The Yukawa interaction is re-derived. Properties of the S-matrix are investigated, while the theory of transition rates is developed in an appendix. Conservation laws are applied, and quark configurations are examined. The effective weak point-coupling is derived. The basic elements of SU(2) symmetry are examined in a problem. Another appendix describes neutrino mixing.

Chapter 8 is on special relativity, with many problems supporting and enhancing the discussion. Several striking applications of Lorentz contraction and time dilation are given. Lorentz scalars are examined. The covariant form of Maxwell’s equations is derived, as well as that of Newton’s law for a charged particle in an E-M field. Several applications of relativistic kinematics are studied, including particle production, elastic scattering, and Compton scattering. A series of problems complements the discussion in the text, and develops the theory of white dwarf stars in the non-relativistic limit (NRL). Available programs again allow the reader to integrate the resulting non-linear differential equations.

Chapter 9 is concerned with relativistic quantum mechanics. Here several exercises give the reader some facility with the Dirac equation and Dirac spinors, supported by an appendix. Problems show how the non-relativistic reduction of the Dirac equation leads to the correct magnetic moment and spin-orbit interaction of the electron. A similar reduction exhibits the main features of the scalar-vector theory of nuclear interactions. The essential elements of the vector–axial-vector (V-A) theory of the weak interactions are illustrated. One problem develops invariant phase space. Another illustrates the kinematics of the quark-parton model and Bjorken scaling.

Chapter 10 is on general relativity. The Doppler shift is first derived in special relativity. Problems then develop the calculus of variations, Hamilton’s equation, and the Euler-Lagrange equation for the dynamical path, all important background for both mechanics and general relativity.⁴ Exercises are presented on time dilation in the Schwarzschild metric and properties of the horizon in the Robertson-Walker metric (with k = 0).

Chapter 11 is on quantum fluids. One problem examines both the sound and critical velocities in a condensed Bose gas. Another involves the numerical integration of the non-linear Gross-Pitaevskii equation for the density distribution in a vortex with unit circulation in that fluid. An exercise concerns London’s phenomenological equation for a superconductor and the corresponding derivation of the penetration depth. Properties of the BCS gap equation in a superconductor are examined in another problem. The Schrödinger equation for a particle in a magnetic field is derived, which provides the basis for the discussion of flux quantization in the text.

The final chapter 12 is on quantum fields. The quantization of the motion of the string serves as our elementary model of a quantum field, and the problems guide the reader through the details of just how this is accomplished. Our previous analysis of the creation and destruction operators stands us in good stead here. Inclusion of a higher bending correction in the string provides an example of a non-linear interaction in quantum field theory. Additional problems work through the quantization of the E-M field and of the Dirac field, where anticommutation relations must be imposed on the creation and destruction operators. There are exercises that obtain the transition rate for an arbitrary photon transition. The cos² θ/2 factor in the Mott scattering of an electron is derived from the Dirac spinors. The quantum field formulation of the non-relativistic many-body problem is investigated, and an appendix supplies many important underlying results for non-relativistic many-body systems. Finally, an exercise develops the lagrangian density, action, and Lagrange’s equation for the string, which exhibits the basics of continuum mechanics and field theory.

After this overview, we proceed to the solutions of the problems.

¹There is a nice irony in the parallel statement, “At the end of the 20th century, one could take pride in the fact that the laws of physics were now understood.”

²Two subsequent volumes in this modern physics series have since been published: Advanced Modern Physics: Theoretical Foundations [Walecka (2010)], and Topics in Modern Physics: Theoretical Foundations [Walecka (2013)].

³There are also problems in all but two appendices, whose solutions are included here.

⁴See [Walecka (2007)].

Chapter 2

Classical Physics

Problem 2.1 Write, or obtain, a computer program that iterates the finite difference Eqs. (2.6) for a given set of initial conditions. It is always good practice to first convert the problem to dimensionless variables. Examine the following cases:

(a) A one-dimensional simple harmonic oscillator moving in the x-direction with F = −κx and initial conditions x₀ = a and [dx/dt]₀ = 0. Use variables ζ = x/a and

(b) A particle performing vertical motion in the upward...

Table of contents

• Cover
• Halftitle
• Title Page
• Copyright Page
• Preface
• Contents
• 1 Introduction
• 2 Classical Physics
• 3 Some Contradictions
• 4 Quantum Mechanics
• 5 Atomic Physics
• 6 Nuclear Physics
• 7 Particle Physics
• 8 Special Relativity
• 9 Relativistic Quantum Mechanics
• 10 General Relativity
• 11 Quantum Fluids
• 12 Quantum Fields
• Appendix A Mathematica Program for Problem 2.5
• Appendix B Matrices
• Appendix C Fourier Series and Fourier Integrals
• Appendix D Some Thermodynamics
• Appendix E Some Statistical Mechanics
• Appendix F Some Vector Calculus
• Appendix G Black Body Flux
• Appendix H Wave Functions for Identical Particles
• Appendix I Transition Rate
• Appendix J Neutrino Mixing
• Appendix K Units
• Bibliography
• Index