Oscillator And Pendulum With A Random Mass

Moshe Gitterman

• Publisher: WSPC
• Year: 2015
• eBook ISBN: 9789814630764
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

Stochastic descriptions of a harmonic oscillator can be obtained by adding additive noise, or/and three types of multiplicative noise: random frequency, random damping and random mass. The first three types of noise were intensively studied in many published articles. In this book the fourth case, that of random mass, is considered in the context of the harmonic oscillator and its immediate nonlinear generalization — the pendulum. To our knowledge it is the first book fully dedicated to this problem.

Two interrelated methods, the Langevin equation and the Fokker–Planck equations, as well as the Lyapunov stability method are used for the mathematical analysis. After a short introduction, the two main parts of the book describe the different properties of the random harmonic oscillator and the random pendulum with random masses. As an example, the stochastic resonance is studied, where the noise plays an unusual role, increasing the applied weak periodic signal, and also the vibration resonance in dynamic systems, where the role of noise is played by the second high-frequency periodic signal.

First and second averaged moments have been calculated for a system with different types of additive and multiplicative noises, which define the stability of a system. The calculations have been extended to two multiplicative noises and to quadratic noise. This book is useful for students and scientists working in different fields of statistical physics.

Contents:

• Introduction
• Oscillator with Random Mass
• Pendulum with a Random Mass

Readership: Students and researchers working in statistical physics.
Key Features:

• The first book dedicated specially to this new field
• Provides pedagogical presentation
• Contains applications to many different problems

Chapter 1

Introduction

A particle of mass m which is displaced from its equilibrium position at x = 0 is subject to a restoring attractive force and a viscous force which, in first approximation, are proportional to the displacement and velocity, respectively. Thus, for an one-dimensional system, Newton’s law gives

where 2γ/m is the damping rate and ω/m^1/2 is the intrinsic frequency. The solution of this equation is

where

If the harmonic oscillator is subject to an external periodic force A exp(iΩt),

then the complete solution of this equation consists of solution (2) of the homogeneous equation (1) and the following solution of the non-homogeneous equation,

The last equation indicates the possibility of a (dynamic) resonance, when the external frequency Ω approaches the intrinsic frequency ω/m^1/2.

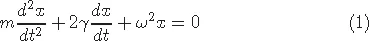
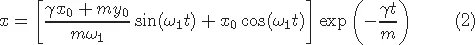
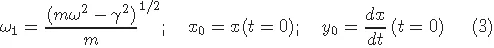
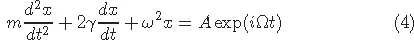
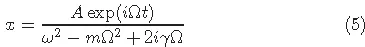
1.1Harmonic oscillator with external noise

In the foregoing we considered a pure mechanical system (zero temperature). For non-zero temperatures, the dynamic equation (1) has to be supplemented by the thermal noise

where η(t) is the random variable with zero mean, 〈η(t)〉 = 0, and variance 〈η²(t)〉, which for thermal noise satisfies the fluctuation-dissipation theorem 〈η²(t)〉 = 4γκT, where κ is the Boltzmann constant [2]. The latter simply means that the power entering the system from the external force must be entirely dissipated and given off to the thermostat in order that the equilibrium state of the system not be disturbed. Another way to justify the validity of Eq. (6) is as follows: in considering only one (slow) mode x(t) of a complex system, one may take into account the influence of other (fast) modes by introducing a random force into dynamic equation with no special requirements for the value of 〈η²(t)〉.

Upon averaging Eq. (6), one finds that the first moment is given by Eq. (2) while the second moment 〈x²(t)〉 for white noise 〈η²(t)〉 = D is defined by the variance,

For m = 1, dichotomous noise of strength σ² and inverse correlation length λ, the variance reaches the following stationary (t → ∞) value

which for white noise is reduced to

Both equations (7) and (8) were obtained already in 1945 [3].

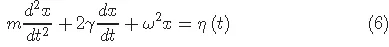
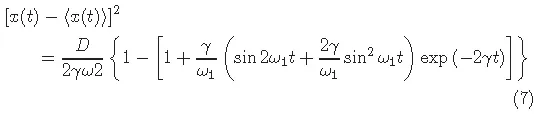
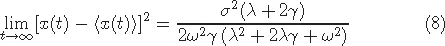
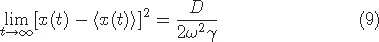
1.2Ito-Stratonovich dilemma

In spite of the fact that the stochastic differential equations were introduced more than a hundred years ago, there are still many interesting problems concerning these equations. We consider here the Ito-Stratonovich dilemma, using the generalized Schlogl model as an example [4], which is described by the following equation,

where ν is an arbitrary number and ξ(t) is white noise with the correlator

The Langevin equation (10) is not completely defined due to the Ito–Stratonovich dilemma, namely, it is not clear which value of t one has to insert in the δ-function (11) and afterwards in the probability distribution. The two possibilities are: before the jump (Ito) or the averaged of before and after the jump (Stratonovich). This choice is very important since it leads to different Fokker-Planck equation for the probability distribution P(x, t) [5]. The first is described by the dynamic equation of the form

and the second by the equation

Another important factor which defines the behavior of a system is the value of ν.

1.For ν = 0, there are three steady states for β > 0, namely, x₀ = 0 (unstable) and

(stable), and one stable state for β < 0, namely, x₀ = 0.

2.For ν > 0, multiplicative noise has an attractive effect, i.e., it attracts the probability P(r, t) to unstable steady state, whereas for ν < 0, the noise term makes system more stable.

3.The stationary probability distribution P(x) (at t → ∞) is defined by the competition between the noise and the damping terms in Eq. (10), which define in going and outgoing energy, respectively, i.e., by three numbers, ν, β and D. In the Stratonovich approach [4] P (x) = C exp ...

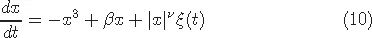
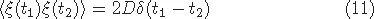
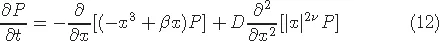
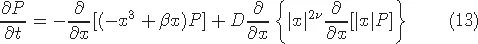
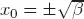
Table of contents

• Cover Page
• Title
• Copyright
• Preface
• 1. Introduction
• 2. Oscillator with a Random Mass
• 3. Pendulum with a Random Mass
• References
• Index