Measure Theory and Functional Analysis

Nik Weaver

• Publisher: WSPC
• Year: 2013
• ISBN:
  9789814508582
• Topic: Mathematik
• Subtopic: Mathematik Allgemein

This book provides an introduction to measure theory and functional analysis suitable for a beginning graduate course, and is based on notes the author had developed over several years of teaching such a course. It is unique in placing special emphasis on the separable setting, which allows for a simultaneously more detailed and more elementary exposition, and for its rapid progression into advanced topics in the spectral theory of families of self-adjoint operators. The author's notion of measurable Hilbert bundles is used to give the spectral theorem a particularly elegant formulation not to be found in other textbooks on the subject.

Request Inspection Copy

Contents:

• Topological Spaces
• Measure and Integration
• Banach Spaces
• Dual Banach Spaces
• Spectral Theory

Readership: Graduates students in mathematics (pure and applied) in their first or second year, graduate students in physics or engineering, and economics.
Key Features:

• A very readable and thorough treatment of the core material in measure theory and functional analysis which cuts a clear path to advanced results in the spectral theory of families of commuting self-adjoint operators, avoiding side topics of lesser importance
• Presents the author's elegant formulation of the spectral theorem in terms of his notion of Hilbert bundles, not available in comparable textbooks
• Uniquely firm emphasis on the separable case allows for a simultaneously more detailed and more elementary exposition
• Includes over 150 exercises

Chapter 1

Topological Spaces

1.1 Countability

We adopt the convention that 0 is not a natural number; thus N = {1, 2, 3, …}.

Definition 1.1. A set is countably infinite if there is a bijection between it and N. It is countable if it is either finite or countably infinite. It is uncountable if it is not countable.

Countability conditions of various types will be assumed liberally throughout this book. Assuming that a set is countable can be very convenient because this means that its elements can be indexed as (a_n), with n ranging either from 1 to N for some N or from 1 to ∞, in either case giving us the ability to deal with them sequentially. Actually, the hypotheses we impose usually will not assert that the main set of interest is itself countable, but rather that in some way its structure is determined by a countable amount of information. This informal comment might make more sense after we discuss separability and second countability in Section 1.4.

Clearly N is countably infinite, since it is trivially in bijection with itself. The set of even natural numbers is also countably infinite via the bijection n

2n, and as the set of odd natural numbers is obviously in bijection with the set of even natural numbers, it is countably infinite too.

This shows that a countably infinite set (the natural numbers) can be split up into two countably infinite subsets (the even numbers and the odd numbers). Conversely, with a moment’s thought it also shows that the union of two disjoint countably infinite sets will again be countably infinite: we can put one set in bijection with the even numbers and the other in bijection with the odd numbers, and then combine the two maps to establish a bijection between the union of the two sets and N. For instance, we can use this idea to show that the set of integers Z is countably infinite. Define f : Z → N by

this is a bijection that matches the positive integers with the even natural numbers and the negative integers and zero with the odd natural numbers.

Next we observe that subsets and images of countable sets are always countable.

Proposition 1.2. Let A be a countable set.

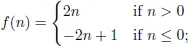
(a)	Any subset of A is countable.
(b)	Any surjective image of A is countable.

Proof. (a) We take it as known that any subset of a finite set is finite, so assume A is countably infinite. Let f : N → A be a bijection and let B be any subset of A. If B is finite we are done, so assume B is infinite. Then f^–1(B) must be an infinite subset of N, so it has a smallest element, a second smallest element, etc. Let n₁ be the smallest element of f^–1(B), n₂ the next smallest, and so on; then the map k

f(n_k) is a bijection between N and B. So B is countably infinite.

(b) Suppose f : A → B is a surjection. Create a map g : B → A by, for each b ∈ B, letting g(b) be an arbitrary element of f^–1(b). Then g is a bijection between B and a subset of A, and it follows from part (a) that B must be countable.

This proposition illustrates why it is helpful to have a special term (“countable”) for sets which are either finite or countably infinite. It is not true that any subset of a countably infinite set is countably infinite, nor is it true that any surjective image is countably infinite.

Having said that, in analysis the unqualified word “sequence” usually means “infinite sequence”, i.e., a sequence indexed by N...

Table of contents

• Cover Page
• Title Page
• Copyright Page
• Contents
• Preface
• 1. Topological Spaces
• 2. Measure and Integration
• 3. Banach Spaces
• 4. Dual Banach Spaces
• 5. Spectral Theory
• Notation Index
• Subject Index