Information Approach To Mitochondrial Dysfunction, An: Extending Swerdlow's Hypothesis

Extending Swerdlow's Hypothesis

Rodrick Wallace

• Publisher: WSPC
• Year: 2015
• eBook ISBN: 9789814663526
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

The monograph applies sophisticated topological symmetry tools to biological applications of information theory, along with a Black–Scholes model invocation of the Data Rate Theorem which links information and control theories. The focus is on statistical mechanics and other models that explore pathological phase transitions — driven by changes in available rates of mitochondrial free energy — in physiological functions, a cutting-edge topic in the study of chronic disease. One of the key focuses is Alzheimer's disease — a relatively simple canonical example.

Contents:

• Mathematical Preliminaries
• A Symmetry-Breaking Model
• A Data Rate Theorem Model
• A Mutual Information Model
• A Fragment Size Model
• Extending the Perspective
• Embodiment and Environment
• Chronic Inflammation
• What is to be Done?
• Mathematical Appendix

Readership: Graduate students and researchers interested in biological applications of information theory.
Key Features:

• Significantly extends current thinking on Alzheimer's and related chronic diseases

Chapter 1

Mathematical preliminaries

We begin with some standard results from information theory, make a significant extension based on the homology between information and free energy noted by Feynman (2000) and others that will prove useful in later chapters, and end with a statement of the Data Rate Theorem that connects information and control theories.

1.1 The coding and tuning theorems

Messages from a source, seen as symbols x_j from some alphabet, each having probabilities P_j associated with a random variable X, are ‘encoded’ into the language of a transmission channel, a random variable Y with symbols y_k, having probabilities P_k, possibly with error. Someone receiving the symbol y_k then retranslates it (without error) into some x_k, which may or may not be the same as the x_j that was sent.

More formally, the message sent along the channel is characterized by a random variable X having the distribution P(X = x_j) = P_j, j = 1, ..., M.

The channel through which the message is sent is characterized by a second random variable Y having the distribution P(Y = y_k) = P_k, k = 1, ..., L.

Let the joint probability distribution of X and Y be defined as P(X = x_j, Y = y_k) = P(x_j, y_k) = P_j,k, and the conditional probability of Y given X as P(Y = y_k|X = x_j) = P(Y_k|x_j).

Then the Shannon uncertainty of X and Y independently and the joint uncertainty of X and Y together are defined respectively as

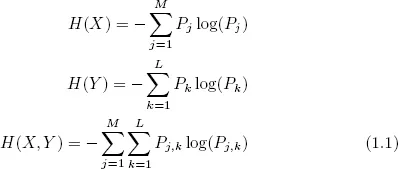
The conditional uncertainty of Y given X is defined as

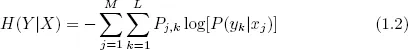
For any two stochastic variates X and Y, H(Y) ≥ H(Y|X), as knowledge of X generally gives some knowledge of Y. Equality occurs only in the case of stochastic independence.

Since P(x_j, y_k) = P(x_j)P(Y_k|x_j), then H(X|Y) = H(X, Y) − H(Y).

The information transmitted by translating the variable X into the channel transmission variable Y – possibly with error – and then retranslating without error the transmitted Y back into X is defined as I(X; Y) H(X) − H(X|Y) = H(X) + H(Y) − H(X, Y). See Cover and Thomas (2006) for details. If there is no uncertainty in X given the channel Y, then there is no loss of information through transmission. In general this will not be true, and in that is the essence of the theory.

Given a fixed vocabulary for the transmitted variable X, and a fixed vocabulary and probability distribution for the channel Y, we may vary the probability distribution of X in such a way as to maximize the information sent. The capacity of the channel is defined as C ≡ max_P(X) I(X; Y), subject to the subsidiary condition that Σ P(X) = 1.

The critical trick of the Shannon Coding Theorem for sending a message with arbitrarily small error along the channel Y at any rate R < C is to encode it in longer and longer ‘typical’ sequences of the variable X; that is, those sequences whose distribution of symbols approximates the probability distribution P(X) above which maximizes C.

If S(n) is the number of such ‘typical’ sequences of length n, then log[S(n)] ≈ nH(X), where H(X) is the uncertainty of the stochastic variable defined above. Some consideration shows that S(n) is much less than the total number of possible messages of length n.

As n → ∞, only a vanishingly small fraction of all possible messages is meaningful in this sense. This, after some development, allows the Coding Theorem to work so well. The prescription is to encode messages in typical sequences, which are sent at very nearly the capacity of the channel. As the encoded messages become longer and longer, their maximum possible rate of transmission without error approaches channel capacity as a limit.

The argument can, however, be turned on its head, in a sense, to provide a ‘tuning theorem’ variant to the coding theorem.

Telephone lines, optical wave guides and the tenuous plasma through which a planetary probe transmits data to earth may all be viewed in traditional information-theoretic terms as a noisy channel around which it is necessary to structure a message so as to attain an optimal error-free transmission rate. Telephone lines, wave guides and interplanetary plasmas are, however, fixed on the timescale of most messages, as are most sociogeographic networks. Indeed, the capacity of a channel is defined by varying the probability distribution of the message X so as to maximize I(X; Y).

Assume, now, however, that some message X so critical that its probability distribution must remain fixed. The trick is to fix the distribution P(X) but now to modify the channel, to tune it, to maximize I(X; Y). A dual channel capacity C* can be defined as C* ≡ max_{P(Y),P(Y |X)} I(X; Y).

But C* = max_{P(Y),P(Y |X)} I(Y ; X) since I(X; Y) = H(X) + H(Y) − H(X, Y) = I(Y ; X).

Thus, in a formal mathematical sense, the message ‘transmits the channel’, and there will be, according to the Coding Theorem above, a channel distribution P(Y) which maximizes C*.

Thus modifying the channel may be a far more efficient means of ensuring transmission of an important message than encoding that message in a ‘natural’ language which maximizes the rate of transmission of information on a fixed channel.

We have examined the two ...

Table of contents

• Cover Page
• Title
• Copyright
• Preface
• Contents
• 1. Mathematical preliminaries
• 2. A symmetry-breaking model
• 3. A Data Rate Theorem model
• 4. A mutual information model
• 5. A fragment size model
• 6. Extending the perspective
• 7. Embodiment and environment
• 8. Chronic inflammation
• 9. What is to be done?
• 10. Mathematical Appendix
• Bibliography
• Index