Fractional Partial Differential Equations And Their Numerical Solutions

Boling Guo, Xueke Pu, Fenghui Huang

• Publisher: WSPC
• Year: 2015
• eBook ISBN: 9789814667067
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

This book aims to introduce some new trends and results on the study of the fractional differential equations, and to provide a good understanding of this field to beginners who are interested in this field, which is the authors' beautiful hope.

This book describes theoretical and numerical aspects of the fractional partial differential equations, including the authors' researches in this field, such as the fractional Nonlinear Schrödinger equations, fractional Landau–Lifshitz equations and fractional Ginzburg–Landau equations. It also covers enough fundamental knowledge on the fractional derivatives and fractional integrals, and enough background of the fractional PDEs.

Contents:

• Physics Background
• Fractional Calculus and Fractional Differential Equations
• Fractional Partial Differential Equations
• Numerical Approximations in Fractional Calculus
• Numerical Methods for the Fractional Ordinary Differential Equations
• Numerical Methods for Fractional Partial Differential Equations

Readership: Graduate students and researchers in mathematical physics, numerical analysis and computational mathematics.
Key Features:

• This book covers the fundamentals of this field, especially for the beginners
• The book covers new trends and results in this field
• The book covers numerical results, which will be of broad interests to researchers

Chapter 1

Physics Background

Fractional differential equations have profound physical background and rich theory, and are particularly noticeable in recent years. They are equations containing fractional derivative or fractional integrals, which have received great interest across disciplines such as physics, biology and chemistry. More specifically, they are widely used in dynamical systems with chaotic dynamical behavior, quasi-chaotic dynamical systems, the dynamics of complex material or porous media and random walks with memory. The purpose of this chapter is to introduce the origin of the fractional derivative, then introduce some physical background of fractional differential equations. Due to space limitations, this chapter only gives some brief introductions, but these are sufficient to show that the fractional differential equations, including fractional partial differential equations and fractional integral equations, are widely employed in various applied fields. However, the mathematical theory and the numerical algorithms of fractional differential equations need to be further studied. Interested readers can refer to the monographs and literature.

1.1Origin of the fractional derivative

The concepts of integer order derivative and integral are well known. The derivative dⁿy/dxⁿ describes the changes of variable y with respect to variable x, and has a profound physical background. The present problem is how to generalize n into a fraction, even a complex number.

This long-standing problem can be dated back to the letter from L’Hôpital to Leibniz in 1695, in which it is asked what the derivative dⁿy/dxⁿ is when n = 1/2. In the same year, the derivative of general order was mentioned in the letter from Leibniz to J. Bernoulli. The problem was also considered by Euler(1730), Lagrange(1849) et al, and gave some relevant insights. In 1812, by using the concept of integral, Laplace provided a definition of fractional derivative. When y = x^m, employing the gamma function

was derived by Lacroix, which gives

When y = x and

. This is consistent with the so-called Riemann-Liouville fractional derivative.

Soon later, Fourier (1822) gave the definition of fractional derivative through the so-called Fourier transform. Noting that the function f(x) can be expressed as a double integral

and

replacing n with a general ν, and calculating the derivative under the sign of integration, one then generalizes the integer order derivative into the fractional derivative

Consider the Abel integral equation

where f is to be de...

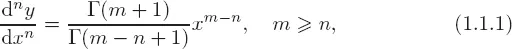
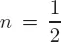
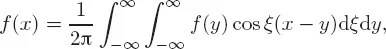
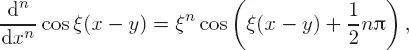
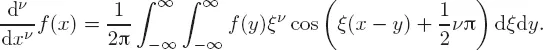
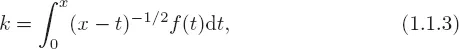
Table of contents

• Cover Page
• Title Page
• Copyright Page
• Preface
• Contents
• 1 Physics Background
• 2 Fractional Calculus and Fractional Differential Equations
• 3 Fractional Partial Differential Equations
• 4 Numerical Approximations in Fractional Calculus
• 5 Numerical Methods for the Fractional Ordinary Differential Equations
• 6 Numerical Methods for Fractional Partial Differential Equations
• Bibliography