Random Matrices And Random Partitions: Normal Convergence

Normal Convergence

Zhonggen Su

• Publisher: WSPC
• Year: 2015
• ISBN:
  9789814612241
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

This book is aimed at graduate students and researchers who are interested in the probability limit theory of random matrices and random partitions. It mainly consists of three parts. Part I is a brief review of classical central limit theorems for sums of independent random variables, martingale differences sequences and Markov chains, etc. These classical theorems are frequently used in the study of random matrices and random partitions. Part II concentrates on the asymptotic distribution theory of Circular Unitary Ensemble and Gaussian Unitary Ensemble, which are prototypes of random matrix theory. It turns out that the classical central limit theorems and methods are applicable in describing asymptotic distributions of various eigenvalue statistics. This is attributed to the nice algebraic structures of models. This part also studies the Circular β Ensembles and Hermitian β Ensembles. Part III is devoted to the study of random uniform and Plancherel partitions. There is a surprising similarity between random matrices and random integer partitions from the viewpoint of asymptotic distribution theory, though it is difficult to find any direct link between the two finite models. A remarkable point is the conditioning argument in each model. Through enlarging the probability space, we run into independent geometric random variables as well as determinantal point processes with discrete Bessel kernels.

This book treats only second-order normal fluctuations for primary random variables from two classes of special random models. It is written in a clear, concise and pedagogical way. It may be read as an introductory text to further study probability theory of general random matrices, random partitions and even random point processes.

This book is aimed at graduate students and researchers who are interested in the probability limit theory of random matrices and random partitions. It mainly consists of three parts. Part I is a brief review of classical central limit theorems for sums of independent random variables, martingale differences sequences and Markov chains, etc. These classical theorems are frequently used in the study of random matrices and random partitions. Part II concentrates on the asymptotic distribution theory of Circular Unitary Ensemble and Gaussian Unitary Ensemble, which are prototypes of random matrix theory. It turns out that the classical central limit theorems and methods are applicable in describing asymptotic distributions of various eigenvalue statistics. This is attributed to the nice algebraic structures of models. This part also studies the Circular β Ensembles and Hermitian β Ensembles. Part III is devoted to the study of random uniform and Plancherel partitions. There is a surprising similarity between random matrices and random integer partitions from the viewpoint of asymptotic distribution theory, though it is difficult to find any direct link between the two finite models. A remarkable point is the conditioning argument in each model. Through enlarging the probability space, we run into independent geometric random variables as well as determinantal point processes with discrete Bessel kernels.

This book treats only second-order normal fluctuations for primary random variables from two classes of special random models. It is written in a clear, concise and pedagogical way. It may be read as an introductory text to further study probability theory of general random matrices, random partitions and even random point processes.

Contents:

• Normal Convergence
• Circular Unitary Ensemble
• Gaussian Unitary Ensemble
• Random Uniform Partitions
• Random Plancherel Partitions

Key Features:

• The book treats only two special models of random matrices, that is, Circular and Gaussian Unitary Ensembles, and the focus is on second-order fluctuations of primary eigenvalue statistics. So all theorems and propositions can be stated and proved in a clear and concise language
• In a companion part, the book also treats two special models of random integerpartitions, namely, random uniform and Plancherel partitions. It exhibits a surprising similarity between random matrices and random partitions from the viewpoint of asymptotic distribution theory, though there is no direct link between finite models
• The limit distributions of most statistics of interest are obtained by reducing to classical central limit theorems for sums of independent random variables, martingale sequences and Markov chains. So the book is easily accessible to readers that are familiar with a standard probability theory textbook

Chapter 1

Normal Convergence

1.1Classical central limit theorems

Throughout the book, unless otherwise specified, we assume that (Ω,

, P) is a large enough probability space to support all random variables of study. E will denote mathematical expectation with respect to P.

Let us begin with Bernoulli’s law, which is widely recognized as the first mathematical theorem in the history of probability theory. In modern terminology, the Bernoulli law reads as follows. Assume that ξ_n, n ≥ 1 is a sequence of independent and identically distributed (i.i.d.) random variables, P(ξ_n = 1) = p and P(ξ_n = 0) = 1 − p, where 0 < p < 1. Denote

. Then we have

In other words, for any ε > 0,

It is this law that first provide a mathematically rigorous interpretation about the meaning of probability p that an event A occurs in a random experiment. To get a feeling of the true value p (unknown), what we need to do is to repeat independently a trial n times (n large enough) and to count the number of A occurring. According to the law, the larger n is, the higher the precision is.

Having the Bernoulli law, it is natural to ask how accurate the frequency S_n/n can approximate the probability p, how many times one should repeat the trial to attain the specified precision, that is, how big n should be.

With this problem in mind, De Moivre considered the case p = 1/2 and proved the following statement:

Later on, Laplace further extended the work of De Moivre to the case p ≠ 1/2 to obtain

Formulas (1.2) and (1.3) are now known as De Moivre-Laplace central limit theorem (CLT).

Note ES_n = np, Var(S_n) = np(1 − p). So (S_n − np)/

is a normalized random variable with mean zero and variance one. Denote

. This is a very nice function from the viewpoint of function analysis. It is sometimes called bell curve since its graph looks like a bell, as shown in Figure 1.1.

Fig. 1.1 Bell curve

The...

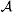
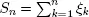
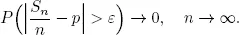
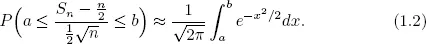
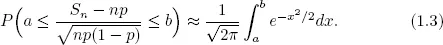
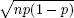
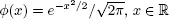
Table of contents

• Cover Page
• Title Page
• Copyright Page
• Dedication Page
• Contents
• Preface
• 1. Normal Convergence
• 2. Circular Unitary Ensemble
• 3. Gaussian Unitary Ensemble
• 4. Random Uniform Partitions
• 5. Random Plancherel Partitions
• Bibliography
• Index