Probability Theory

A Complete One-Semester Course

Nikolai Dokuchaev

• Publisher: WSPC
• Year: 2015
• ISBN:
  9789814678056
• Topic: Mathématiques
• Subtopic: Mathématiques appliquées

This book provides a systematic, self-sufficient and yet short presentation of the mainstream topics on introductory Probability Theory with some selected topics from Mathematical Statistics. It is suitable for a 10- to 14-week course for second- or third-year undergraduate students in Science, Mathematics, Statistics, Finance, or Economics, who have completed some introductory course in Calculus. There is a sufficient number of problems and solutions to cover weekly tutorials.

Request Inspection Copy

Contents:

• Probability
• Random Variables
• Joint Distributions
• Transformations of the Distributions
• Expectation of Random Variables
• Variance and Covariance
• Conditional Expectations
• Moment Generating Functions
• Analysis of Some Important Distributions
• Limit Theorems
• Statistical Inference: Point Estimation
• Statistical Inference: Interval Estimation
• Appendices:
  • Solutions for the Problems for Weeks 1–12
  • Sample Problems for Final Exams
  • Some Bonus Challenging Problems
  • Statistical Tables

Readership: Undergraduate students, teachers and lecturers in Mathematics and Statistics.
Key Features:

• This book is short and comprehensive
• The amount of material is exactly as is needed for a one-semester course
• There are enough problems with solutions to cover weekly tutorials
• Supplementary PDF files of presentation slides are provided for lecturers who adopt the textbook

Week 1. Probability

In this chapter, we introduce random events, probability of events, and conditional probability. In addition, we consider examples where probability can be calculated using combinatorial methods.

1.1Probability axioms

The probability theory gives numerical values for possible scenarios under uncertainty. For a particular problem, one has to construct a probability model. For this, one has to select a sample space from a system of events and presume that each event can be assigned with a certain probability for which it can occur.

The sample space

The set of all outcomes in a probability model is called the sample space. It is usually denoted by Ω, and an element of Ω are usually denoted by ω.

Example 1.1 Consider the coin tossing game where a coin is thrown in the air and the outcome of either a head or tail is observed. The sample space for this model is the set of all possible outcomes

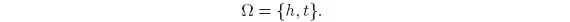
Example 1.2 A coin is thrown twice, and a sequence of heads and tails is observed. The sample space is the set of all possible outcomes

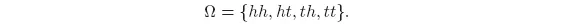
It can be noted that a sample choice of Ω is not uniquely defined for a particular problem. Usually, it is convenient to consider the smallest possible set. However, it is also acceptable to consider larger sets Ω, including some “impossible” outcomes. This could be done for convenience or just to shorten the descriptions.

Example 1.3 Tomorrow’s exchange rate for AUD/USD can be regarded as an outcome. In this case, we could select the set

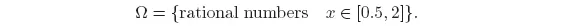
For this example, we could also take Ω = R, including some “impossible” outcomes.

Definition 1.4 Sets of outcomes (i.e. subsets of Ω) are called events (or random events).

The standard operations of the set theory can be applied directly into probability theory.

Let A and B be two events. The union of these two events is the event C that either A occurs or B occurs (or both occur). In terms of the set theory, C = A ∪ B. It can also be written as “C = A or B”, or “C = A + B”.

The intersection of two events, C = A ∩ B, is the event that both A and B occur. It can also be written as “C = A and B”, or “C = A · B”.

The complement of an event, A^c, is the event that A does not occur, or A^c = Ω\A.

A ⊂ B means that A implies B (i.e., if A occurs then B occurs).

The empty set (denoted by

) is the set with no elements: it is an event that does not include any outcomes. If A ∩ B =

(i.e., these events cannot occur at the same time), A ...

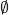
Table of contents

• Cover Page
• Title Page
• Copyright Page
• Contents
• Preface
• Acknowledgments
• Week 1. Probability
• Week 2. Random Variables
• Week 3. Joint Distributions
• Week 4. Transformations of the Distributions
• Week 5: Expectation of Random Variables
• Week 6. Variance and Covariance
• Week 7. Conditional Expectations
• Week 8. Moment Generating Functions
• Week 9. Analysis of Some Important Distributions
• Week 10. Limit Theorems
• Week 11. Statistical Inference: Point Estimation
• Week 12. Statistical Inference: Interval Estimation
• Appendix 1: Solutions for the Problems for Weeks 1-12
• Appendix 2: Sample Problems for Final Exams
• Appendix 3: Some Bonus Challenging Problems
• Appendix 4: Statistical Tables
• Bibliography
• Index
• Legend of Notations and Abbreviations