The Numerical Solution of Ordinary and Partial Differential Equations

Granville Sewell

• Publisher: WSPC
• Year: 2014
• ISBN:
  9789814635110
• Edition: 3
• Topic: Mathematik
• Subtopic: Angewandte Mathematik

This book presents methods for the computational solution of differential equations, both ordinary and partial, time-dependent and steady-state. Finite difference methods are introduced and analyzed in the first four chapters, and finite element methods are studied in chapter five. A very general-purpose and widely-used finite element program, PDE2D, which implements many of the methods studied in the earlier chapters, is presented and documented in Appendix A.

The book contains the relevant theory and error analysis for most of the methods studied, but also emphasizes the practical aspects involved in implementing the methods. Students using this book will actually see and write programs (FORTRAN or MATLAB) for solving ordinary and partial differential equations, using both finite differences and finite elements. In addition, they will be able to solve very difficult partial differential equations using the software PDE2D, presented in Appendix A. PDE2D solves very general steady-state, time-dependent and eigenvalue PDE systems, in 1D intervals, general 2D regions, and a wide range of simple 3D regions.

Contents:

• Direct Solution of Linear Systems
• Initial Value Ordinary Differential Equations
• The Initial Value Diffusion Problem
• The Initial Value Transport and Wave Problems
• Boundary Value Problems
• The Finite Element Methods
• Appendix A — Solving PDEs with PDE2D
• Appendix B — The Fourier Stability Method
• Appendix C — MATLAB Programs
• Appendix D — Answers to Selected Exercises

Readership: Undergraduate, graduate students and researchers.
Key Features:

• The discussion of stability, absolute stability and stiffness in Chapter 1 is clearer than in other texts
• Students will actually learn to write programs solving a range of simple PDEs using the finite element method in chapter 5
• In Appendix A, students will be able to solve quite difficult PDEs, using the author's software package, PDE2D. (a free version is available which solves small to moderate sized problems)

1
Initial Value Ordinary Differential Equations

1.0 Introduction

Differential equations are often divided into two classes, ordinary and partial, according to the number of independent variables, and studied separately. A more meaningful division, however, is between initial value problems, which usually model time-dependent phenomena, and boundary value problems, which generally model steady-state systems. The differences between initial value and boundary value problems, and the similarities within each of these classes, are even more striking when numerical methods for these problems are considered.

The identification of initial value problems with time dependency and of boundary value problems with a steady-state condition is helpful in understanding some of the differences in the properties of these two types of problems. For example, the solution at any time of a time-dependent problem logically depends only on what has gone on before and not on future events. For a steady-state problem, on the other hand, the solution values at different spatial points may be interdependent. Thus it is not surprising that a time-dependent (initial value) problem can be solved numerically by marching forward in time from the given initial values, while a system of simultaneous algebraic equations must generally be solved to find the solution to a steady-state (boundary value) problem.

It is also clear why initial value problems almost always have unique solutions, while boundary value problems sometimes have many or no solutions. Consider, for example, the general second-order equation mu_tt = f(t, u, u_t), which may be thought of as modeling Newton’s second law, applied to an object whose coordinates are given by the vector u(t). With initial conditions u(0) = u₀, u_t(0) = u₁, under very reasonable smoothness assumptions on the force field f, this problem will always have a unique solution. To find it, one only needs to create the force field described by f and release the object with the prescribed initial position and velocity. The object will find the solution even if we cannot! With boundary conditions u(0) = u₀, u(1) = u₁, there is no guarantee that a unique solution exists, as we are now requiring that the object travel from point u₀ to point u₁ in a prescribed time, under the specified force field, a requirement that may be impossible to satisfy or that may be satisfied by many trajectories. Note that we have just given an example of a time-dependent boundary value problem!

The problem to be studied in this chapter is the first-order initial value ordinary differential equation problem

All of the methods and results of this chapter generalize to systems of first-order equations (u′ = f(t, u), u(0) = u₀) in a straightforward manner, by simply allowing u, f, u₀, and their approximations to be vector quantities. The introduction of additional dependent variables does not have any of the complicating effects that the introduction of additional independent variables has.

Furthermore, higher-order initial value problems are easily converted into first-order systems. For example, the second-order problem

can be reduced to a system of two first-order equations by introducing the auxiliary variable v ≡ du ∕ dt:

Thus it is sufficient to study only the single first-order equation u′ = f(t,u).

1.1 Euler’s Method

Since by definition (du ∕ dt)(t) = lim_{h → 0}(u(t + h) − u(t)) ∕ h, the simplest and most obvious approach to solving du ∕ dt = f(t,u) is to approximate it by

where h is a small but nonzero stepsize. (The calculus student learns to take l...

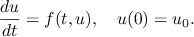
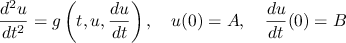
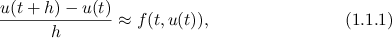
Table of contents

• Cover
• Halftitle
• Title
• Copyright
• Dedication
• Contents
• Preface
• 0 Direct Solution of Linear Systems
• 1 Initial Value Ordinary Differential Equations
• 2 The Initial Value Diffusion Problem
• 3 The Initial Value Transport and Wave Problems
• 4 Boundary Value Problems
• 5 The Finite Element Method
• Appendix A—Solving PDEs with PDE2D
• Appendix B—The Fourier Stability Method
• Appendix C—MATLAB Programs
• Appendix D—Answers to Selected Exercises
• References
• Index