
- 344 pages
- English
- ePUB (mobile friendly)
- Available on iOS & Android
Change of Time and Change of Measure
About this book
Change of Time and Change of Measure provides a comprehensive account of two topics that are of particular significance in both theoretical and applied stochastics: random change of time and change of probability law.
Random change of time is key to understanding the nature of various stochastic processes, and gives rise to interesting mathematical results and insights of importance for the modeling and interpretation of empirically observed dynamic processes. Change of probability law is a technique for solving central questions in mathematical finance, and also has a considerable role in insurance mathematics, large deviation theory, and other fields.
The book comprehensively collects and integrates results from a number of scattered sources in the literature and discusses the importance of the results relative to the existing literature, particularly with regard to mathematical finance.
In this Second Edition a Chapter 13 entitled 'A Wider View' has been added. This outlines some of the developments that have taken place in the area of Change of Time and Change of Measure since the publication of the First Edition. Most of these developments have their root in the study of the Statistical Theory of Turbulence rather than in Financial Mathematics and Econometrics, and they form part of the new research area termed 'Ambit Stochastics'.
Request Inspection Copy
Contents:
- Random Change of Time
- Integral Representations and Change of Time in Stochastic Integrals
- Semimartingales: Basic Notions, Structures, Elements of Stochastic Analysis
- Stochastic Exponential and Stochastic Logarithm. Cumulant Processes
- Processes with Independent Increments. Lévy Processes
- Change of Measure. General Facts
- Change of Measure in Models Based on Lévy Processes
- Change of Time in Semimartingale Models and Models Based on Brownian Motion and Lévy Processes
- Conditionally Gaussian Distributions and Stochastic Volatility Models for the Discrete-time Case
- Martingale Measures in the Stochastic Theory of Arbitrage
- Change of Measure in Option Pricing
- Conditionally Brownian and Lévy Processes. Stochastic Volatility Models
- A Wider View. Ambit Processes and Fields, and Volatility/Intermittency
Readership: Mathematical researchers, graduate students and practitioners interested in application of probabilistic theories & stochastic processes to economics & finance, and to turbulence.
Key Features:
- There is no other book on the market with such a specific and in-depth focus on these two main issues of change of time and change of probability law and Lévy measure
- It is invaluable as a textbook for graduate-level courses and students, or a handy reference for researchers and practitioners in financial mathematics and econometrics
- Provides a strong and comprehensive account by drawing together sources from a wide range of books and research papers in the fields of theoretical and applied probability
Frequently asked questions
- Essential is ideal for learners and professionals who enjoy exploring a wide range of subjects. Access the Essential Library with 800,000+ trusted titles and best-sellers across business, personal growth, and the humanities. Includes unlimited reading time and Standard Read Aloud voice.
- Complete: Perfect for advanced learners and researchers needing full, unrestricted access. Unlock 1.4M+ books across hundreds of subjects, including academic and specialized titles. The Complete Plan also includes advanced features like Premium Read Aloud and Research Assistant.
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Information
Chapter 1
Random Change of Time
1.1Basic Definitions
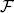
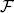
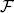
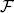
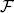
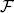
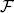
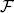
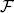
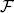
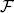
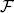
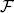
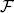
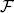
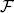
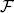
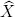
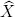
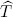
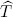
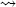
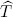
| (a) | (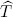 |
Table of contents
- Cover Page
- Title page
- Copyright
- Foreword
- Foreword1
- Contents
- Introduction
- 1. Random Change of Time
- 2. Integral Representations and Change of Time in Stochastic Integrals
- 3. Semimartingales: Basic Notions, Structures, Elements of Stochastic Analysis
- 4. Stochastic Exponential and Stochastic Logarithm. Cumulant Processes
- 5. Processes with Independent Increments. Lévy Processes
- 6. Change of Measure. General Facts
- 7. Change of Measure in Models Based on Lévy Processes
- 8. Change of Time in Semimartingale Models and Models Based on Brownian Motion and Lévy Processes
- 9. Conditionally Gaussian Distributions and Stochastic Volatility Models for the Discrete-time Case
- 10. Martingale Measures in the Stochastic Theory of Arbitrage
- 11. Change of Measure in Option Pricing
- 12. Conditionally Brownian and Lévy Processes. Stochastic Volatility Models
- 13. A Wider View. Ambit Processes and Fields, and Volatility/Intermittency
- Afterword
- Afterword to the Second Edition
- Bibliography
- Index