Methods and Techniques for Proving Inequalities

Yong Su, Bin Xiong

• Publisher: WSPC
• Year: 2015
• eBook ISBN: 9789814696470
• Topic: Mathematics
• Subtopic: Algebra
• Index: Mathematics

In China, lots of excellent maths students take an active interest in various maths contests and the best six senior high school students will be selected to form the IMO National Team to compete in the International Mathematical Olympiad. In the past ten years China's IMO Team has achieved outstanding results — they won the first place almost every year.

The authors are coaches of China's IMO National Team, whose students have won many gold medals many times in IMO.

This book is part of the Mathematical Olympiad Series which discusses several aspects related to maths contests, such as algebra, number theory, combinatorics, graph theory and geometry. The book explains many basic techniques for proving inequalities such as direct comparison, method of magnifying and reducing, substitution method, construction method, and so on.

Request Inspection Copy

In China, lots of excellent maths students take an active interest in various maths contests and the best six senior high school students will be selected to form the IMO National Team to compete in the International Mathematical Olympiad. In the past ten years China's IMO Team has achieved outstanding results — they won the first place almost every year.

The authors are coaches of China's IMO National Team, whose students have won many gold medals many times in IMO.

This book is part of the Mathematical Olympiad Series which discusses several aspects related to maths contests, such as algebra, number theory, combinatorics, graph theory and geometry. The book explains many basic techniques for proving inequalities such as direct comparison, method of magnifying and reducing, substitution method, construction method, and so on.

Request Inspection Copy

Readership: Senior high school students engaged in math contests, math teachers, undergraduates of math major and math enthusiasts.
Key Features:

• China has performed outstandingly in IMO and the book gathers from the tutorial experience of many excellent teachers
• The author is one of the leading experts in aspects of maths contests in China as the coach of China's IMO National Team
• The Chinese version of the book has been very popular

Chapter 1

Basic Techniques for Proving Inequalities

Among quantities observed in real life, equal relationship is local and relative while unequal relationship is universal and absolute. The exact nature of inequality is the studying of unequal relationship among quantities.

Now, for two quantities we can always compare them, or try to show one of them is greater than the other: in other words, we need to prove an inequality. The techniques for proving an inequality varies from case to case and often require some basic inequalities such as the famous AM-GM Inequality and the Cauchy-Schwarz Inequality; other techniques even involve some more advanced algebraic rearrangements. In this chapter, we introduce some of the most basic techniques for proving inequalities.

1.1Direct Comparison

Naturally, we have two ways to compare two quantities:

(1) Compare by subtraction: to show A ≥ B, it suffices to show A − B ≥ 0;

(2) Compare by division: say B > 0, to show A ≥ B, it suffices to show

When we use the above two methods to compare two quantities, usually some forms of rearrangements is required. For example, factorization, separating and combining terms are some of...

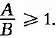
Table of contents

• Cover Page
• Title
• Copyright
• Contents
• Chapter 1 Basic Techniques for Proving Inequalities
• Chapter 2 Identical Transformation of the Sum
• Chapter 3 Substitution Method
• Chapter 4 Proof by Contradiction
• Chapter 5 Construction Method
• Chapter 6 Local Inequality
• Chapter 7 Mathematical Induction and Inequality
• Chapter 8 Inequality and Extremum for Multi-Variable Function
• Chapter 9 Special Techniques for Proving Inequalities
• Detailed Solutions to Exercises