Functional Analysis

Entering Hilbert Space

Vagn Lundsgaard Hansen

• Publisher: WSPC
• Year: 2015
• eBook ISBN: 9789814733946
• Edition: 2
• Topic: Mathematics
• Subtopic: Calculus
• Index: Mathematics

This book presents basic elements of the theory of Hilbert spaces and operators on Hilbert spaces, culminating in a proof of the spectral theorem for compact, self-adjoint operators on separable Hilbert spaces. It exhibits a construction of the space of p th power Lebesgue integrable functions by a completion procedure with respect to a suitable norm in a space of continuous functions, including proofs of the basic inequalities of Hölder and Minkowski. The L p -spaces thereby emerges in direct analogy with a construction of the real numbers from the rational numbers. This allows grasping the main ideas more rapidly. Other important Banach spaces arising from function spaces and sequence spaces are also treated.

In this second edition, I have expanded the material on normed vector spaces and their operators presented in Chapter 1 to include proofs of the Open Mapping Theorem, the Closed Graph Theorem and the Hahn–Banach Theorem.

The material on operators between normed vector spaces is further expanded in a new Chapter 6, which presents the basic elements of the theory of Fredholm operators on general Banach spaces, not only on Hilbert spaces. This requires that we develop the theory of dual operators between Banach spaces to replace the use of adjoint operators between Hilbert spaces.

With the addition of the new material on normed vector spaces and their operators, the book can serve as a general introduction to functional analysis viewed as a theory of infinite dimensional linear spaces and linear operators acting on them.

Request Inspection Copy

This book presents basic elements of the theory of Hilbert spaces and operators on Hilbert spaces, culminating in a proof of the spectral theorem for compact, self-adjoint operators on separable Hilbert spaces. It exhibits a construction of the space of p th power Lebesgue integrable functions by a completion procedure with respect to a suitable norm in a space of continuous functions, including proofs of the basic inequalities of Hölder and Minkowski. The L p -spaces thereby emerges in direct analogy with a construction of the real numbers from the rational numbers. This allows grasping the main ideas more rapidly. Other important Banach spaces arising from function spaces and sequence spaces are also treated.

In this second edition, I have expanded the material on normed vector spaces and their operators presented in Chapter 1 to include proofs of the Open Mapping Theorem, the Closed Graph Theorem and the Hahn–Banach Theorem.

The material on operators between normed vector spaces is further expanded in a new Chapter 6, which presents the basic elements of the theory of Fredholm operators on general Banach spaces, not only on Hilbert spaces. This requires that we develop the theory of dual operators between Banach spaces to replace the use of adjoint operators between Hilbert spaces.

With the addition of the new material on normed vector spaces and their operators, the book can serve as a general introduction to functional analysis viewed as a theory of infinite dimensional linear spaces and linear operators acting on them.

Request Inspection Copy

Readership: Undergraduates in mathematical and physical sciences, and mechanical, electrical and electronic engineering.
Key Features:

• Offers a fast construction of the Lebesgue integrable functions. These mathematical objects are introduced as added limits for sequences of continuous functions and are thereby experienced by students as being no more mysterious than the real numbers constructed as limits of sequences of rational numbers. No compromises are made with respect to mathematical rigor
• Contains a comprehensive discussion of the question about existence of a Schauder basis in a Hilbert space and the relation of this question to the topological notion of separability
• Contains a complete treatment of the spectral theorem for compact, self-adjoint linear operators on separable Hilbert spaces
• Gives an introduction to Fredholm theory. Fredholm operators are of interest far beyond functional analysis. They also play a significant role in theoretical physics, differential geometry and topology with the famous Index Theorem proved by Michael Atiyah and Isadore Singer in 1963 as a highlight

Chapter 1

Basic Elements of Metric Topology

A major step forward in the development of functional analysis was taken around 1900 when mathematicians in their search for solutions to variational problems began to consider functions with specified properties as elements in spaces of functions of similar type. This was enhanced by the creation of new mathematical structures, such as metric spaces and more generally, topological spaces, which came to be known as general, or pointset, topology. Using these new structures a firm basis could be established for fundamental notions from analysis such as convergence of sequences and continuity of functions.

In this chapter we review briefly necessary basic elements of general topology of spaces involving a metric structure. We develop basic material on normed vector spaces and their operators with full proofs of the Open Mapping Theorem, the Closed Graph Theorem and the Hahn-Banach Theorem.

1.1Metric spaces

A distance function (or a metric) on a set M is a function

which to any pair of points x, y ∈ M associates a real number d(x, y), called the distance from x to y. Furthermore, to get a reasonable notion of distance, it has proved fruitful to require that the following three conditions are satisfied:

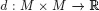
MET 1	(positive definite) d(x, y) ≥ 0, for all x, y ∈ M, x = y.
MET 2	(symmetry) d(x, y) = d(y, x), for all x, y ∈ M.
MET 3	(the triangle inequality) d(x, z) ≤ d(x, y) + d(y, z), for all x, y, z ∈ M.

Definition 1.1.1. A metric on a set M is a function

satisfying the conditions MET 1, MET 2, MET 3.

A pair (M, d) consisting of a set M together with a specific metric d on M is called a metric space.

Remark 1.1.2. The same set M can be equipped with several different metrics, in which case the corresponding metric spaces are counted as different.

When the context leaves no doubt as to which metric is being considered, usually the metric is not mentioned explicitly.

The idea of metric spaces was introduced by the French mathematician Maurice Fréchet (1878–1973) in his doctoral thesis of 1906.

A few examples of metric spaces are in order.

Example 1.1.3. Consider the set of real ...

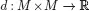
Table of contents

• Cover page
• Title page
• Copyright page
• Dedication
• Preface to the Second Edition
• Preface to the First Edition
• Preliminary Notions
• Contents
• 1. Basic Elements of Metric Topology
• 2. New Types of Function Spaces
• 3. Theory of Hilbert Spaces
• 4. Operators on Hilbert Spaces
• 5. Spectral Theory
• 6. Fredholm Theory
• Exercises
• Bibliography
• List of Symbols
• Index